Geometrical characteristics of uniportal VATS
Introduction
The surgical technique and current indications of Uniportal Video-Assisted Thoracic Surgery (VATS) have already been described in detail (1,2). Nevertheless, thoracic surgeons do not completely understand the potential use of Uniportal VATS because they do not completely understand the advantages of the geometrical uniportal approach.
Notes of geometry
The geometric construction of VATS is almost similar to the real word since there is a profound interplay between the natural world and the laws (3) of thought. The most fundamental and firmly accepted parts of our general scientific knowledge of the world involve mathematical models. Geometry is the field of mathematics whose main source of intuition is human visual perception. Vision is one of our most important senses giving contact with the world outside of us. In other words, visual perception is the construction, inspired by images recorded by early vision, of hypotheses which produce visual images that match physical reality in accordance with our previously acquired experience of the same reality.
According to Herodotus, geometry developed first in Egypt: “They say that king Sesostri (2000 B.C.) distributed the land among all of the Egyptians, each one having an equal lot in a square shape, and from these subdivisions obtained tribute, having imposed an annual payment. If the river bore away a part, the owner announced the loss, and officials were sent to observe the extent to which the plot had been diminished for the purpose of adjusting the tribute payment. It is my feeling that this indicates the invention of geometry here, prior to its passing to Greece”.
Since the primary school, we are familiar with Euclidean geometry and with its well description of our world. Euclid of Alexandria was the most prominent mathematician of antiquity best known for his treatise on mathematics “The Elements”, a compilation of knowledge that became the core of mathematical teaching for 2000 years. In “The Elements” the building blocks of geometry are described, such as points (figures without size, a location in space), lines (a set of infinitely many points, with one dimension and no thickness that goes on forever in both directions), planes (with a length, a width and without thickness, that extends infinitely in two-dimensions), and rays (a part of a line that starts at a point that extends infinitely in one direction). Also, five postulates are described in “The Elements”. The fifth postulate, so-called parallel, states that one and only one line can be drawn through a point parallel to a given line. It was not until the 19th century that this postulate was dropped and non-Euclidean geometries were studied. In Euclidean geometry, the sides of objects have lengths, intersecting lines determine angles between them, and two lines are said to be parallel if they lie in the same plane and never meet (1).
Geometry of three port access thoracoscopy
When we consider the imaging during a VATS operation, it becomes clear that Euclidean geometry is insufficient: lengths and angles are no longer preserved, and parallel lines may intersect. Lobacevskian geometry discards Euclid’s 5th postulate replacing it with the following one: given a line and a point not on in, there are infinitely lines going through the given point that is parallel to the given line.
Therefore, the classic three-port approach, in which the lozenge geometric configuration allows maximal convergence of operative instruments from each side of target lesion, produces an interference with the optical source. In coordinate geometry, a lozenge is similar to an ordinary parallelogram with the addition that its position on the coordinate plane is known (Figure 1).
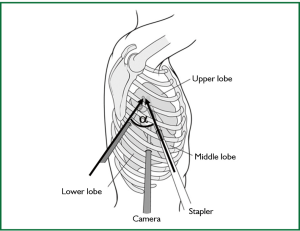
Geometry of single access thoracoscopy
Projective geometry well reflects the imaging process of VATS, because it allows a much larger class of transformations than just translations and rotations, a class which includes perspective projections. We must start from Euclidean geometry to understand the reason why knowledge of projective geometry is required to appreciate the optical advantages of Uniportal VATS. Two lines (two-dimensional geometry) almost always meet in a point. A common linguistic artifact for getting around this is to say that parallel lines meet “at infinity” enhancing the Euclidean plane by the addition of these points at infinity where parallel lines meet, and resolving the difficulty with infinity by calling them “ideal” points. By adding these points at infinity, the familiar Euclidean space is transformed into a new type of geometric object, the projective space. The projective space is an extension of Euclidean space in which two lines always meet in a point, at infinity. It turns out that the point at infinity in the two-dimensional projective space form a line, usually called the line at infinity. In the three-dimension vision they form the plane at infinity. In the real world, there are no points at infinity, namely the line at infinity in the flat image and the plane at infinity in the world (4). For this reason, although we usually work with projective spaces, we are aware that the line and plane at infinity are in some way special. Generally, we try to have it both ways by treating all points in projective space as equals when it suits us, and singling out the line at infinity in space or the plane at infinity in the image when that becomes necessary. The Uniportal approach requires the translation of the thoracoscope instruments 90° along a sagittal plane, thus bringing the operative instruments to address the target lesion from a vertical, caudo-cranial perspective. To avoid mutual interference, the use of reticulating instruments is of paramount importance for their ability to rotate the stem and the jaws independently on different planes and with multiple angles. The shift from three-dimensional world to a two-dimensional image is a projection process in which we lose one dimension. The usual way of modeling this process is by central projection in which a ray from a point in space is drawn from a three-dimensional world point through a fixed point in space, the so-called “centre of projection”. This ray will intersect a specific plane in space chosen as the image plane. The intersection of the ray with the image plane represents the image of the point. If the three-dimensional structure lies on a plane then there is no drop in dimension. For the purposes of image projection, it is possible to consider all points along such a ray as being equal. We can go one step further, and think of the ray through the projection centre as representing the image point. Thus, the set of all image points is the same as the set of rays through the camera centre. Thus two images taken from the same point in space are projectively equivalent (5).
Therefore, Uniportal VATS technique is based on a completely different geometric concept compared with conventional three-port VATS (6). In fact, the approach to the target lesion in the lung is substantially similar to the approach that the surgeon would use in open surgery (2). Because the visualization of the target lesion occurs along the same axis, the target lesion in the lung would be elevated with forceps perpendicularly from the parenchymal profile and resected by applying a stapler (or a curved clamp and overseen) at the base of this newly created, cone-shaped parenchymal area (1). The instruments inserted parallel to videothoracoscope mimic inside the chest the maneuvers performed during open surgery (6). In the Uniportal VATS approach, the target lesion is located in a projective plane with homogeneous coordinates and represents the point at infinity (Figure 2). The epipolar geometric explanation of the advantages of Uniportal VATS is that, in the projective plane, the sagittal approach to target lesion preserves the depth of intraoperative visualization provided by the currently available two-dimensional video monitors (6).
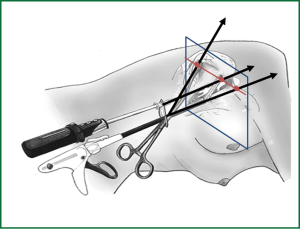
Conclusions
Standard three-port VATS has a geometric configuration of lozenge that interfere with optical source with a creation of a new optical plane for the genesis of a dihedral or torsion angle not favorable with monitors. On the contrary, the Uniportal VATS approach the lesion along a sagittal plane; the target lesion is reached forma a caudo-cranial perspectives that realize a projective plane that preserve the depth of intraoperative visualization. In Uniportal VATS instruments are parallel lines drawn on the plane that enables surgeon to bring operative fulcrum inside the chest.
Acknowledgements
Disclosure: The authors declare no conflict of interest.
References
- Rocco G, Martin-Ucar A, Passera E. Uniportal VATS wedge pulmonary resections. Ann Thorac Surg 2004;77:726-8. [PubMed]
- Rocco G. Single-port video-assisted thoracic surgery (Uniportal) in the routine general thoracic surgical practice. Op Techn Thorac Cardiovasc Surg 2009;14:326-35.
- Dillen F, Verstraelen L. eds. Handbook of Differential Geometry. Amsterdam: North Holland, 2000.
- Gregory RL. Eye and Brain, the Psychology of Seeing. Oxford: Oxford University Press, 1998.
- Browder FE, Mac Lane S. The Relevance of Mathematics. New York: Vintage Books, 1980.
- Bertolaccini L, Rizzardi G, Terzi A. Single-port video-assisted thoracic surgery resection: the Copernican revolution of a geometrical approach in thoracic surgery? Interact Cardiovasc Thorac Surg 2011;12:516. [PubMed]


