Basic statistics (the fundamental concepts)
Introduction
An appreciation and understanding of statistics is import to all practising clinicians, not simply researchers. This is because mathematics is the fundamental basis to which we base clinical decisions, usually with reference to the benefit in relation to risk. Unless a clinician has a basic understanding of statistics, he or she will never be in a position to question healthcare management decisions that have been handed down from generation to generation, will not be able to conduct research effectively nor evaluate the validity of published evidence (usually making an assumption that most published work is either all good or all bad).
Summarising and presenting data
Why is it important?
Summarising data is usually the fundamental basis to which the background data on a cohort is described. Often it is too cumbersome to describe all the features of each individual that is studied and becomes impossible to do so with large numbers.
How is it done?
In general data are summarised with two measures, a statement of “central tendency” followed by a statement of “variation”. In general data are divided into continuous (normal and non-normally distributed) or categorical (binary or multiple categories).
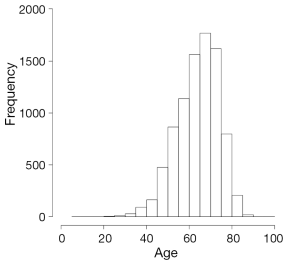
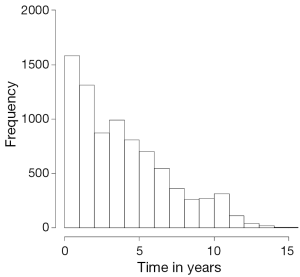
It is important to separate continuous data in normal and non-normally distributed because the summary measures used are different. When data is normally distributed (e.g., age, Figure 1) we can use summary measures such as the mean and standard deviation. Because of the distribution of the data, we can use “shortcuts” to calculate the spread, for example we know that 95.45% of the observations will lie between two standard deviations of the mean. This is not the same for non-normally distributed data (e.g., length of follow up, Figure 2), which is summarised as median and interquartile range.
Categorical data can be more straightforward. It can be a binary category (e.g., gender with only two outcomes, male or female) or multiple categories (e.g., colour). Categorical data is summarised as frequency and percentage e.g., 32 (34%).
What is the relevance?
If you apply the mean and standard deviation wrongly to describe the data that is not normally distributed, for example mean length of follow up of 4 years, standard deviation of 3 years, and then the data is interpreted as 95.45% of the observations will lie between −2 and 10 years. It is impossible to have a length of follow up of −2 years!
It is important to appreciate outcomes such as cancer stage (I-IV) should be treated as categorical and not continuous, because a cancer stage of III does not imply that the outcome is 3-fold worse than a cancer stage of I.
Comparing single outcomes and single variables
Why is it important?
One of the most basic aspects evaluating improvements in healthcare or surgical techniques is by comparing the outcomes of two (or more) different procedures.
How is it done?
Like summary measures, statistical tests used to compare outcomes are based on calculations that make assumptions on the data distributions. Therefore it is important that the correct test is applied to the corresponding data distributions. In general, when comparing two different and independent outcomes, a t-test is used to compare normally distributed continuous data, the Mann-Whitney or a Wilcoxon rank sum test is used to compare continuous non-normally distributed data and the Chi-square test (or Fisher’s exact test if the numbers are very small) is used to compare categorical data.
The statistical test generates a P value for example 0.05, which correctly interpreted means that if the test was done (over and over) many times, the likelihood of observing the difference (or more extreme value) due to chance is 5%.
What is the relevance?
It is important to use the correct test to each distribution, for example if a Chi-square test is used when the observed (more correctly predicted) values are very low (e.g., 1/25) then the chances of achieving a statistically significance result is (incorrectly) easier.
Many clinicians do not understand how to interpret a P value. Firstly, it implies that the “test” will be performed over and over again many time (long run frequency), and this is clearly not the case in clinical practice. Secondly, many take it as an absolute value in that a P value of 0.04 is significant but a P value of 0.06 is not. To appreciate that attitude is saying that a 4% and 6% chance of rain tomorrow is extremely and completely different, clearly for all intents and purposed there is no difference between 4-6%. In fact, my own opinion is that there really is not much difference between 5% or 10% (i.e., P=0.10). Another lesser known fact is that the P value is driven by the size of the data, therefore differences between 9/10 versus 7/10 may not be significant (P=0.582), but the P value for the difference between 9,000/10,000 versus 7,000/10,000 is (P
Comparing single outcomes with multiple variables
Why is it important?
So far, we have only discussed comparing one outcomes and one variable (e.g., death versus surgical group), however outcomes can be influenced by multiple variables. Regression analyses are multivariable methods that allow us to compare an outcome adjusting for multiple different variables (e.g., death versus surgical group, age and lung function).
How is it done?
There are a family of regression methods appropriate to the type and distribution of the outcome of interest. Linear regression is the basic model that is applied to a continuous normally distributed outcome (e.g., serum potassium) and the measures of association are usually given in the same units as the outcome measure (e.g., each year of age increases serum potassium by 0.011 mmol/L). For binary outcomes, logistic regression is used and the measure of association is given as an odds ratio (the odds of an event happening versus the odds of an event not happening). The odds ratio is a difficult ratio for most to interpret (unless you are an experienced gambler) and often it is (incorrectly) interpreted as a relative risk. The discussion is out of the scope of this article, but as an illustration the two ratios of 2/4 and 1/4 is expressed as a relative risk of 2/4÷1/4=2 and an odds ratio of 2/2÷1/3=3. Therefore the output of a measure of association in a logistic regression model is interpreted for example in men, the odds ratio of developing ischaemic heart disease is 4.3 compared to women.
What is the relevance?
It is important to be able to appreciate the correct regression method for the correct type and distribution of outcomes. Often clinicians who are less experienced try to convert outcomes from continuous to binary simply to apply a different method of analyses for example, instead of using a linear regression for serum potassium, they would convert it into high versus low serum potassium (above or below 4.5 mmol/L) and apply logistic regression methods.
Advanced statistical methods
Why is it important?
As data become more complex, correct handling and analyses is important to be able to get valid results.
How is it done?
So far, we have discussed comparing one outcome with one variable and with multiple variables that does not take time or missing data into account. The commonly used data in medical literature that includes missing data and time is survival analyses. This is when patients are followed up to a time point and are alive (censored) or died. The most common regression method in this circumstance is the use of the Cox proportional hazards regression where time and censoring is taken into account. The measure of association is a hazard ratio that refers to the relative risk of death.
As data becomes more complicated, more sophisticated methods are applied, such as longitudinal data analyses when multiple time points of interest are analysed, the most common thoracic surgical example is the longitudinal lung function outcomes after lung volume reduction surgery. The analysis needs to take into account, time, irregular time intervals, correlation within each patient, and correlation with time before comparison can be made with another group.
What is the relevance?
If proper statistical methods are not used to account for time and missing data, erroneous conclusions can occur. For example, if a new surgical intervention is introduced and the follow up time is only 1 month compared to the old technique used for over 30 years, with follow up time of 30 years, few deaths will occurs in the new technique group with a follow up time of 1 month compared to the old technique group of 30 years, and a researcher could make the false conclusion that there we statistically significantly less deaths on follow up with the new technique.
Conclusions
This article provides a brief introduction to basic statistical methods and illustrates its use in common clinical scenarios. In addition, pitfalls of incorrect usage have been highlighted. It is not meant to be a substitute for formal training or consultation with a qualified and experienced medical statistician prior to starting any research project.
Acknowledgements
Disclosure: The author declares no conflict of interest.