Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions
Introduction
In December 2019 an outbreak of atypical pneumonia [coronavirus disease 2019 (COVID-19)] occurred in Wuhan, the capital of Hubei Province in mainland China, that was attributed to a novel coronavirus of zoonotic origin [severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2)] (1,2). The outbreak spread rapidly, with over 50,000 cases and 1,000 deaths reported domestically and 603 cases globally (3,4), surpassing the 2003 outbreak of the severe acute respiratory syndrome (SARS) (5). The outbreak coincided with chunyun, the annual period of mass migration for the Spring Festival holidays that was to begin on January 25, 2020. To contain the outbreak, China implemented unprecedented intervention strategies on 23 January, 2020 (6). Whole cities were quarantined, the national holiday was extended, strict measures limiting travel and public gatherings were introduced, public spaces were closed and rigorous temperature monitoring was implemented nationwide. These control measures have caused significant disruption to the social and economic structure in China and globally. However, it is unknown whether these policies have had an impact, and how long they should remain in place. It is thus critical to assess the effects of these control measures on the epidemic progression for the benefit of global expectation. Here, we used a modified susceptible-exposed-infected-removed (SEIR) epidemiological model that incorporates the domestic migration data before and after January 23 and the most recent COVID-19 epidemiological data to predict the epidemic progression. We also corroborated our model prediction using a machine-learning artificial intelligence (AI) approach that was trained on the 2003 SARS coronavirus outbreak data.
Methods
Data sources
The most recent epidemiological data based on daily COVID-19 outbreak numbers reported by the National Health Commission of China were retrieved (7). Migration index based on the daily number of inbound and outbound events by rail, air and road traffic, were sourced from a web-based program (8). The 2003 SARS epidemic data between April and June 2003 across the whole of China retrieved from an archived news-site (SOHU) (9) was used for AI-training.
Modified SEIR model
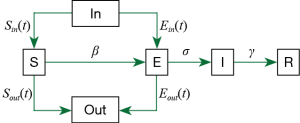
We modified the original SEIR-equation to account for a dynamic Susceptible [S] and Exposed [E] population state by introducing the move-in, In(t) and move-out, Out(t) parameters. Conceptually, the modified model is shown as:
The base model is as follows;
Here, we assume that latent [E] population is asymptomatic but infectious, and [I] refers to the symptomatic and infectious population. The incubation rate, σ is described as the rate by which the exposed individual develops symptoms.
Our modified model is given by;
S(t): The number of susceptible people in a province.
Sin/out(t): Inflow/outflow of susceptible people based on the publicly available daily Migration Index (8).
β1: The rate of transmission for the susceptible to infected.
β2: The rate of transmission for the susceptible to exposed.
r(t): The number of contacts per person per day, related to control policies. Before Jan 23, r = 15, after Jan 23, r = 3, and after March 1, r = 10 (assuming that some form of control policy remains in place to reduce contact rate).
N(t): The total population in a province.
E(t): The number of exposed people (in a province).
Ein/out(t): The number of inflowing/outflowing exposed people (see Supplemental file). We assume all Ein is from Hubei Province.
σ: The incubation rate.
I(t): The number of infected people in a province.
γ: The probability of recovery or death.
R(t): The number of the recovery or death (in a province).
Pout[t]: The probability of the outflowing exposed people (see Supplemental file).
Estimation of model parameters
In order to apply the SEIR model, we need to estimate the parameters β, σ and γ, where β is the product of the people exposed to each day by infected people (k) and the probability of transmission (b) when exposed (i.e., β= kb) and σ is the incubation rate which is the rate of latent individuals becoming symptomatic (average duration of incubation is 1/σ). Because the incubation period of the SARS-CoV-2 has been reported to be between 2 to 14 days (2,10,11,12), we chose the midpoint of 7 days. γ is the average rate of recovery or death in infected populations. Using epidemic data from Hubei, we modeled the skewed SEIR model to determine the probability of transmission (b) which was used to derive β and the probability of recovery or death (γ).
The number of people who stay susceptible in each province is similar to that of its resident population. Of these, there are 57 million in Zhejiang Province, 113 million in Guangdong Province and 60 million in Hubei Province. Finally, we added a 9-day gap period before the provincial data to simulate the infection to diagnosis of the first patient.
With I(t=0)=1, which is available early in the outbreak, N≈S and therefore approximates
Finally, it is simplified to:
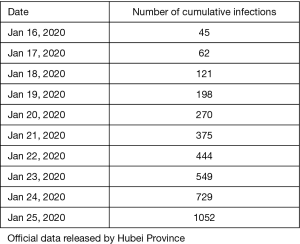
After multiple fitting with data from the table above, we determined b [(95% confidence interval (CI)] to be: 0.05249 (0. 05068–0. 05429). and γ [(95% confidence interval (CI)] to be: 0.154 (95% CI=0.0721-0.238).
We assume that a symptomatic, infectious [I] will be quarantined, therefore k1 =3.
We assume that an asymptomatic, latent [E] will have normal contact, therefore k2 =15.
Therefore, using the b =0.05249,
β1 =3×0.05249=0.15747
β2 =15×0.05249=0.78735
The trends of virus transmission in Zhejiang, Guangdong and Hubei provinces and nationwide were calculated. The data spans vary slightly among the three provinces, with data for Zhejiang and Guangdong provinces encompasses 24 days from January 17, 2020 (date of first report) to February 9, 2020, while the data from Hubei Province encompasses 30 days from January 11, 2020 (date of official confirmation) to February 9, 2020. The effects of public health intervention measures restricting migration was modeled, as was the effect of initiating interventions five days before and after the actual intervention time. We derived the prediction interval interventions implemented on January 23 2020 using Monte Carlo simulation.
Long-Short-Term-Memory (LSTM) model
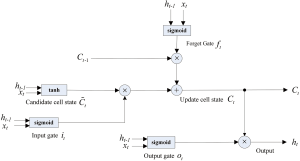
We used the LSTM model, a type of recurrent neural network (RNN) that has been used to process and predict various time series problems to predict numbers of new infections over time. For the basic training dataset, we used the 2003 SARS epidemic statistics, which were only available for cases between April and June of 2003. We incorporated the COVID-19 epidemiological parameters, such as the probability of transmission, incubation rate, the probability of recovery or death and contact number. Because of the relatively small dataset, we developed a simpler network structure to prevent overfitting. The model was optimized using the Adam optimizer and ran for 500 iterations. Details on the development of this algorithm is included in the supplemental material.
Results
Epidemic progression in Hubei, Guangdong and Zhejiang provinces
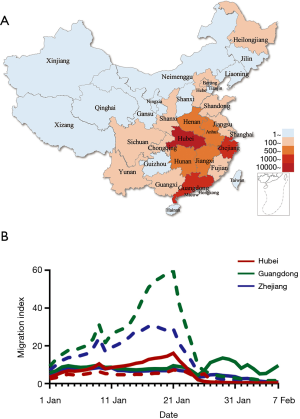
We studied these provinces as they had the largest number of confirmed COVID-19 cases at time of writing (7,8) and a significant migrant population. Confirmed cases of COVID-19 in Hubei, Guangdong and Zhejiang provinces on February 10 were 31,728, 1,177 and 1,117, respectively, representing 80% of total cases nationwide (Figure 1A). The migration index out of Guangdong and Zhejiang province were greater than the inflow and were largest between January 7 and January 23 2020. The migration index into Hubei province was greater than the outflow before January 23, signaling the homeward return of the migrant population for Spring Festival celebration. The enforced public health interventions to limit travels in Hubei province are evident as relatively flat migration curves in comparison to Guangdong and Zhejiang provinces after January 23 2020 (Figure 1B).
SEIR is an epidemiological model used to predict infectious disease dynamics by compartmentalizing the population into four possible states: Susceptible [S], Exposed or latent [E], Infectious [I] or Removed [R]. The proportion of a population in each state is governed by the rate of change between each, β ([S] to [E]), σ ([E] to [I]) and γ ([I] to [R]). We incorporated the migration index [Sin/out(t)] for the previous day, (t) to account for pool of [S(t+1)] at the location of interest into the modified SEIR model, using available 2020 migration index for each province up to the time of the analysis but adjusted the migration index for later dates according to the situation we are simulating. For simulations where travel restriction is stepped down in Guangdong, Zhejiang, China and Hubei, we used the 2019 migration index. We considered the rate of transmission, β between [E] → [S] (β1) to be five-fold that of [I] → [S] (β2).
In Hubei province, where strict quarantine measures are currently in place, we set the migration index to null after February 10 2020. Prior to February 12, cases were reported based on PCR-confirmation. Based on this reporting criteria, our model predicted a single epidemic peak on February 20 with 42,792 (95% CI: 30,149–52,941) cases (Table 1). The outbreak is expected to be nearing its end by late April with total case numbers reaching 59,578 (95% CI: 39,189–66,591). If interventions were delayed, a peak of 11,5061 cases would be reached by February 25 with total case numbers reaching 167,598. Had the interventions been introduced five days earlier, the epidemic peak should have been reached by February 15 2020 and final number of cases would not exceed 25,000 (Figure 2).
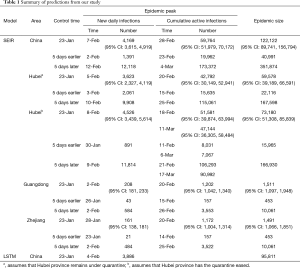
Full table
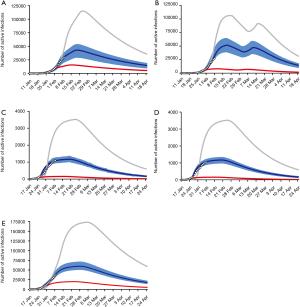
We then considered the situation where quarantine ceased, allowing normal migration. However, expecting that some form of control measure would continue to be in place to reduce social contact, we set the r = 10. We modeled a first peak of 51,581 (95% CI: 39,874–63,994) cases on February 18 and a smaller second peak on March 11 with 47,144 (95% CI: 36,305–58,484) cases. The total epidemic size will be 73,180 (95% CI: 51,308–85,839) cases. If implementation of interventions were delayed by five days, the initial increase in the proportion of exposed cases would have resulted in an exponential increase in infected cases, peaking on February 21 and March 17. There would still be >30,000 active cases predicted at the end of April, by which time there would have been 166,930 cases. Had interventions been implemented five days earlier, the epidemic would have peaked by February 11 with 8,031 cases and a final epidemic size of 15,965 cases should have been expected (Figure 2B).
Because Guangdong and Zhejiang provinces were not in the outbreak epileft, the epidemic sizes are smaller than that in Hubei province. The epidemics in these two provinces would peak by February 20 2020 with 1,202 (95% CI: 1,042–1,340) and 1,172 (95% CI: 1,004–1,314) cases, respectively, and end by mid-April. The total epidemic sizes will be 1,511 (95% CI: 1,097–1,948) and 1,491 (95% CI: 1,066–1,851) cases in Guangdong and Zhejiang provinces, respectively. A five-day delay in government intervention would have resulted in February 26 and 25 peaks with 3,553 and 3,522 cases in Guangdong and Zhejiang provinces, respectively, and a total epidemic size of 10,061 cases in each province. If government control was introduced five days earlier, the epidemic would have been effectively suppressed (Figure 2C,D).
We plotted the actual reported cumulative active infections (circles in Figure 2A,B,C,D) up to February 10 2020 for each province onto our predicted curve and found that there was overall a good fit between our projected and reported data.
Epidemic progression in Mainland China
After implementation of control measures on January 23 2020, the opportunity for spread was decreased. The availability of a large pool of susceptible individuals allowed for a steady increase in the average number of new daily infections. With current interventions, the epidemic is predicted to peak on February 28, with 59,764 (95% CI: 51,979–70,172) cases. The total epidemic size is predicted to be 122,122 (95% CI: 89,741–156,794) cases. If the introduction of interventions was delayed by five days, the transmission coefficient would have been much greater due to the increase in the average number of contacts with an infected person daily. Case numbers would have increased exponentially, peaking on March 4 2020, at 173,372 cases. By end of April the total epidemic size will be 351,874 cases. Were the interventions to be introduced 5 days earlier than they had been, the number of cases nationwide would have been 40,991 (Figure 2E). Similarly, there was also a good fit between actually reported cumulative active infections with our predicted curve.
LSTM prediction for mainland China
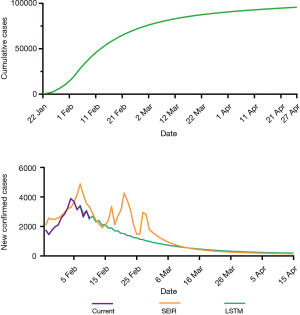
The LSTM model is a type of RNN that was trained using the 2003 SARS epidemic statistics incorporating the COVID-19 epidemiological parameters, such as the probability of transmission, incubation rate, The probability of recovery or death and contact number. The LSTM model predicted that new infections will peak on February 4, resulting in 95,000 cases by the end of April (Figure 3A). We then plotted the number of daily new cases derived from SEIR, LSTM and the actual reported data for China. There was a remarkable fit between the actual number of new confirmed cases and the LSTM-predicted curve between January 22 and the February 10 (Figure 3B). Both the SEIR and LSTM-model predicted a peak of 4,000 daily infection between February 4 and 7. The SEIR model also predicted several smaller peaks of new infections in mid to late February.
Discussion
China declared a Level 1 emergency response, the highest level public health response, to the COVID-19 outbreak on January 15 2020, causing the implementation of control measures nationwide. Aside from locking down the Greater Wuhan area, strict reporting of travel to and from Hubei province was required. Hubei residents were dissuaded from returning to their workplace and even non-Hubei residents who had traveled via Wuhan were required to self-quarantine for 14 days. The effectiveness and necessity of such undertakings have been questioned, particularly with reports that the Greater Wuhan quarantine may have been instituted too late (13,14). Wu et al., predicted that without control measures the epidemic size in Wuhan would reach 75,000 infections by January 25 and the epidemic would peak in April (13). Similarly, Read et al., predicted a peak of 190,000 cases by February 4 without control measures (14). Notably, they predicted that other Chinese cities would experience similar epidemic growth to Wuhan, despite the Greater Wuhan quarantine. However, this has not been the case. Guangdong and Zhejiang, the two most affected provinces after Hubei, only account for 6.6% of all PCR-confirmed cases nationally, owing to quicker enforcement of control measures (Figure S1). The slowed epidemic growth in these two provinces compared to Hubei support the effectiveness of quarantine and control measures. Our model echoed these scenarios, suggesting that a five-day delay in implementation of control measures would have increased the epidemic size three-fold.
The actual epidemic trend since our analyses has fit well with our predicted curve (Figure S2). Guangdong and Zhejiang have reported less than 6 new cases daily in the previous week while the number of new cases in Hubei also appeared to have declined compared to the past weeks. With the migrants beginning to return to Guangdong and Zhejiang (although at a slower rate compared to previous years due to existing restrictions), concerns spark over potential increase in imported cases. Since a considerable day-to-day number of new cases currently remains only in Hubei, it appears less likely that migrants from other provinces would pose significant risks. The continued policy of “early detection” and subsequent isolation might be effective in preventing a second epidemic wave in Guangdong and Zhejiang.
Our study highlighted another key point, the step-down of the quarantine restriction on Hubei will allow an influx of new susceptible individuals, i.e., migrants returning after the Spring Festival holidays, leading to another smaller epidemic peak in Hubei around March 11 2020. Given that substantial resources have since been channeled to Hubei to construct new hospitals and quarantine lefts built to improve medical care and reduce exposure risks, all these are expected to reduce transmission and help mitigate the impact of the potentially forthcoming peak.
The COVID-19 outbreak presents a major challenge in the public health process of epidemic control in a well-connected and densely populated city and the decision of when to implement control measures. The current practice to confirm a COVID-19 infected case relies on two positive test results from the local and city or provincial CDC, a process that requires at least 30 hours (15). On February 12 2020, the Hubei government allowed for case confirmations by clinical diagnosis based on radiologic findings, neutrophil counts and epidemiologic links, resulting in 16,000 cases added to the daily incidence overnight. This consequently muddled nationwide statistics of COVID-19 cases as this approach was not adopted in all other provinces. One could argue that clinical diagnoses may not be accurate, though, the current PCR diagnostic approach also has weaknesses (15). Until further methods such as seroprevalence data are available to estimate true incidence, we can expect that epidemic curves based on PCR confirmation alone likely underestimates the situation in the real world.
Our results in Figure 3 highlight the strength and weaknesses of the two models used in our study. Our modified SEIR model used a seven-day incubation period, which was based on early estimates (2). As known later, the median incubation time prior to symptom onset is three days (11), which is closer to the reported incubation period for SARS, but can range from 0 to 24 days. We tested the model sensitivity to different incubation time and found that shorter incubation time will accelerate the epidemic peak and result in a smaller epidemic size (Figure S3). This may explain the remarkable fit between the real and LSTM-predicted curves, as well as the lag to the epidemic peak predicted by the SEIR-model. Conversely, the SARS epidemic data used for machine-training were derived from cases reported between April and June 2003, which seems to be a limited dataset for longer-term prediction.
Our model did not account for other factors that may increase confirmed case numbers, such as diagnostic capacity. The Wuhan municipal government recently announced a policy on testing every suspected case and staggering the return of migrant workers (16). If the Wuhan government is able to increase its testing capacity, we will expect to see a continuous peak or even second peak, despite controlling the inflow of returning migrants. Another limitation to our study is that we did not account for seasonal influences. Change in temperatures due to seasonality was postulated to be important for the dissipation of the SARS epidemic in Guangdong (17). Following this logic with COVID-19, the epidemic would hopefully subside earlier in Guangdong province compared to Zhejiang and Hubei.
Conclusions
Our dynamic SEIR model was effective in predicting the COVID-19 epidemic peaks and sizes. Furthermore, an AI-based model trained on past SARS dataset also shows promise for future prediction of the epidemics. The implementation of control measures on January 23 was predicted to reduce the COVID-19 epidemic size in China, and the policy of strict monitoring and early detection should remain in place until the end of April 2020.
Supplementary
Supplemental method
SEIR model establishment process
Total data categories and sources
The most recent epidemiological data of the COVID-19 outbreak in mainland China was retrieved based on daily numbers reported by the National Health Commission of China (7). Migration rates, the daily number of inbound and outbound events by rail, air and road traffic, were sourced from a web-based program (8).
Model building process
A classic epidemiological model to study the dynamics of an infectious disease is the Susceptible (S)- Exposed (E)- Infectious (I)- Recovered (R) model.
The transmission rate, β, controls the rate of spread which represents the probability of transmitting disease between a susceptible and an infectious individual. The incubation rate, σ, is the rate of latent individuals becoming symptomatic (average duration of incubation is 1/σ) (set as 7 days). The probability of recovery or death, γ, is the average rate of recovery or death in infected populations.
The classic SEIR equation assumes a constant susceptible [S] population size with constant birth and death rate across all compartments. In the actual situation, this population is dynamic, as there will be a large number of people moving in and out of each city and epidemic-associated deaths. We modified the original form to introduce move-in, In(t)and move-out, Out(t) and r(t), which is the contact rate before and after the implementation of control policies. We considered the rate of transmission, β: for the susceptible to infected to be β1, for the susceptible to exposed to be β2.
SEIR brings the differential expression of the migrated population:
Where:
β1: The rate of transmission for the susceptible to infected.
β2: The rate of transmission for the susceptible to exposed.
In(city)(t): The number of people flowing from different cities in Hubei to other provinces
Pin(city)(t): The probability of the inflow of people from different cities in Hubei to other provinces that is Exposed
EinHB(t): Number of Exposed flowing from Hubei to other provinces
SinHB(t): The number of Susceptible people flowing from Hubei to other provinces
Ein/out(t): The number of inflowing/outflowing exposed people. We assume all Ein is from Hubei
Sin/out(t): Inflow/outflow of susceptible people based on the publicly available daily Migration Index
In(t): Population inflow to a Province
Out(t): Population outflow from a Province
Pout(t): Probability of latent people flowing out of Province
N(t): Total population in a Province
r(t): Number of contacts per person per day, related to control policies
A(city) (t): Number of new confirmed cases in a city
PO (city) (t): The total population of a city
e: Correlation factor between the number of new diagnoses and the number of exposed cases
Probability of a latent in a Province population:
The number of latent people flowing into a Province from Hubei is:
Before February 8th, we assumed that the country's latent population into a Province are all from Hubei:
The number of susceptible people flowing into Province from all over Hubei is:
The number of normal people flowing into Province as a whole is as:
The number of latent flowing out of a Province is:
The number of normal outflows from a Province is:
Province total population:
Number of normal people in a Province:
Number of latents in a Province:
Number of Infectious persons in a Province:
Number of Recovered in the Province:
Long-Short-Term Memory Networks (LSTM) model building
Time series analysis was based on data obtained by systematic observation. The goal of this trend prediction was to predict the sequence of factors, such as the number of infections over time. According to the different methods of analysis, the time series prediction model can be divided into simple sequential average, weighted sequential average, moving average, weighted moving average, trend prediction method, exponential smoothing method, seasonal trend prediction method, market life cycle prediction method, etc. In recent years, with the study of machine learning, especially deep learning theory, LSTM, a special Recurrent Neural Network, has been used to process and predict various time series problems. In view of the traditional time series model used in the past to fit the transmission process of the SARS-CoV, this study used the 2003 SARS-CoV infection statistics, using the SEIR classic infectious disease model to adjust the probability of transmission, incubation rate, the probability of recovery or death and contact number obtain a basic training data set. The LSTM time series model was established to study the trend of virus transmission and to predict the transmission of COVID-19.
Types and sources of data
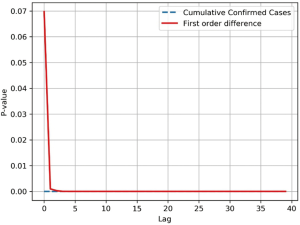
Time series of the cumulative number of SARS-CoV infections in 2003 were collected and the overall correlation of the sequence was tested. The time series data of cumulative infections was as high as the rising trend is a non-smooth sequence, therefore the sequence is processed by a first-order differential, which transforms the sequence into a stable sequence of number of new infections per day (Figure S4).

The Ljung-Box (LB) test was performed on both sequences at the same time. The Q statistic for the LB test was calculated as follows;
The LB test was used to determine if , the self-correlation of the sequence in the m-order hysteresis, is significant, or if the sequence is noise. The Q statistic is subject to the box distribution with a freedom of m, and T is the sample size, which is the correlation coefficient of the sample l-order lag. When the two sequences were delayed beyond the 5th order, the P-value dropped below the confidence level of 0.05, indicating a significant self-regression relationship with heteronormativeity (Figure S5). Therefore, it is valid to use the cumulative number of SARS-CoV infections and daily new infections datasets for the study and prediction of our time series models. In order to effectively capture the timing of virus infection, it is necessary to divide the data by time slice. This model sets the time slice step of the data sample to 3, which uses the number of infections in the first three days as an argument and the number of infections in the next day as regression variables, thus establishing the original data into a dataset for model training.
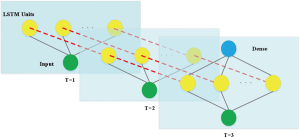
Model building process
The LSTM long-term memory network proposed by Hochreiter and Schmidhuber (1997) is widely used to solve time series problems with long-dependent characteristics. The LSTM network model was used to predict the trend of the new coronavirus outbreak in 2019-nCoV (Figure S6).
In order to evaluate the difference between the predicted and real values of cases and to find the gradient drop direction to reduce the gap, the loss function of this model was set to mean square error (MSE), as per the following equation:
Because the dataset is small, a simpler network structure was adopted to prevent overfitting, by using a LSTM neural network and a full-connection layer (Figure S7).
Neural network parameter selection
The model selected the adam optimizer, using a training wheel designed for 500 rounds, batch size of one and the loss function selected in the above-mentioned MSE.
AI learning process
The 2003 SARS-CoV cumulative number of confirmed infections first-order differential treatment was used to obtain the daily number of new confirmed cases and interpolation was used to adjust the outliers. Time series data was then obtained by setting the sequence length time sliding window step. Using time slice data, the LSTM model was used as input for training, looping the training 500 times and saving the trained LSTM model. The number of new infections of COVID-19 nationally from January 22 to February 7, was then entered into the trained LSTM model to obtain a national forecast for new infections and a trend chart for cumulative infections over 80 days after February 8 (Figure S8).
Acknowledgments
We thank Yujia Cheng, Bingyi Ji and Bifeng Xu from Hengqin WhaleMed Technology Co., Ltd. for technical support.
Funding: This work was supported by the Science Research Project of the Guangdong Province (Nanshan Zhong).
Footnote
Provenance and Peer Review: This article was submitted to JTD as a revised version along with the incisive peer review comments after rejection from another esteemed journal. Given the revisions and the wide concern and pressing importance of research relating to COVID-19, the article was managed via the rapid communication pathway and underwent internal review within 24 hours.
Conflicts of Interest:NZ serves as the unpaid Editor-in Chief of Journal of Thoracic Disease. JH serves as the unpaid Executive Editor-in-Chief of Journal of Thoracic Disease. WL serves as an unpaid Editorial Board Member (Thoracic Surgery) of Journal of Thoracic Disease. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Zhou P, Yang XL, Wang XG, et al. A pneumonia outbreak associated with a new coronavirus of probable bat origin. Nature 2020. [Epub ahead of print]. [Crossref] [PubMed]
- Li Q, Guan X, Wu P, et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus-Infected Pneumonia. N Engl J Med 2020. [Epub ahead of print]. [Crossref] [PubMed]
- Real-time big data report on the epidemic (in Chinese) 2020. Available online: https://voice.baidu.com/act/newpneumonia/newpneumonia/?from=osari_aladin_top1
- Coronavirus disease 2019 (COVID-19) Situation Report–25 2020. Available online: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200214-sitrep-25-covid-19.pdf?sfvrsn=61dda7d_2
- Situation Updates - SARS: Update 95 - Chronology of a serial killer 2003. Available online: https://www.who.int/csr/don/2003_06_18/en/
- 2019 Data from spring festival (in Chinese) 2019. Available online: http://news.sina.com.cn/c/2019-02-04/doc-ihrfqzka3579637.shtml
- Situation report (in Chinese) 2020. Available online: http://www.nhc.gov.cn/xcs/yqtb/list_gzbd.shtml
- Baidu qianxi (in Chinese) 2020 Available online: https://qianxi.baidu.com/
- Combatting SARS (in Chinese) 2003. Available online: http://news.sohu.com/57/26/subject206252657.shtml
- Backer JA, Klinkenberg D, Wallinga J. Incubation period of 2019 novel coronavirus (2019-nCoV) infections among travellers from Wuhan, China, 20–28 January 2020. Euro Surveill 2020;25:2000062. [Crossref] [PubMed]
- Guan WJ, Ni ZY, Hu Y, et al. Clinical characteristics of 2019 novel coronavirus infection in China. medRxiv 2020. doi: 10.1101/2020.02.06.20020974. [Crossref]
- Wang W, Tang J, Wei F. Updated understanding of the outbreak of 2019 novel coronavirus (2019-nCoV) in Wuhan, China. J Med Virol 2020;92:441-7. [Crossref] [PubMed]
- Wu JT, Leung K, Leung GM. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet 2020. [Epub ahead of print]. [Crossref] [PubMed]
- Read JM, Bridgen JRE, Cummings DAT, et al. Novel coronavirus 2019-nCoV: early estimation of epidemiological parameters and epidemic predictions. medRxiv 2020. doi: 10.1101/2020.01.23.20018549. [Crossref]
- Novel coronavirus diagnosis and treatment protocol (in Chinese) 2020. Available online: http://www.nhc.gov.cn/xcs/zhengcwj/202002/d4b895337e19445f8d728fcaf1e3e13a/files/ab6bec7f93e64e7f998d802991203cd6.pdf
- Pneumonia epidemic prevention and control work of new coronavirus deployed in our city 2019. Available online: http://www.wuhan.gov.cn/2019_web/whyw/202001/t20200123_304083.html
- Lin K, Yee-Tak Fong D, Zhu B, et al. Environmental factors on the SARS epidemic: air temperature, passage of time and multiplicative effect of hospital infection. Epidemiol Infect 2006;134:223-30. [Crossref] [PubMed]