A new solution model for cardiac medical image segmentation

Introduction

Computed tomography (CT) scanning and magnetic resonance imaging (MRI) are the most widely used modalities for clarifying cardiac-related ailments in clinic. The procedure carried out by a cardiologist is according to a visual testing of the images. For cardiologists to complete the treatment course, images from optical examination based on a manual delineation of human organs is required. This method however is subjective, time-consuming, and more prone to error. Thus, calculation methods have a critical role in more precisely sorting medical images.

In image processing by computer, sorting the images can be exceedingly challenging, but numerous applications can be derived from this process including those in medical imaging investigation, video surveillance, and biological, military, and network areas. Towards this end, many methods have been proposed including wavelet transform (1), rule optimization with region growing (2), enhanced suppressed fuzzy c-means (3), improved water shed transform (4), multi-threshold with artificial immune systems (5), graph cut (6,7), and active contour models (ACM). The ACM is a method that significantly decreases the use of energy and that uses snaxel points to monitor the segmentation processing. Based on the form of the object, the spline works by assessing the inner and outer powers. ACM has been used in clinical centers as a medical instrument across many applications, including in the segmentation of breast lesions (8), breast tumors (9), the prostate (10), and intravascular ultrasound images (11). Traditional ACM models have two disadvantages. The first disadvantage is that, the initialization of control points should be placed approaching the determined object; otherwise, these points cannot be integrated. The second drawback is that, in the regional minima, the chosen snaxel deteriorates, and consequently the obtained outcomes are not reliable. In order to overcome these disadvantages, investigators have proposed different approaches, all which simultaneously function with ACM; among the proposed models, water balloons (12), statistical methods (13,14), graph cut (15), genetic algorithms (16), differential evolution (17), and particle swarm optimization (PSO) (18) are the most important. Common large searching windows are usually actively produced based on the primary location of the monitoring points. Correspondingly, Abedinia’s study Abedinia et al. (19) proposed a hybrid snake model through applying the PSO velocity formula in the ACM. Based on the obtained results, the function of the two presented PSO methods is appropriate, because the ACM is more active in the regional minima errors. PSO is most the widely used approach for disentangling the optimization errors in the attached spaces (20,21).

The PSO approach has more in common with other newly evolved techniques because it controls a range of randomly selected answers, known as “swarm”. These potential solutions or answers usually apply to particles instead of individuals, and fitness performances are applied in order to assess them. The proposed technique represents an instrument which was originally inspired by the rational and social behaviors of bird groups or fish schools. In order to share obtained data from the distance of particles, two main ways of connecting are considered. In the first method, the best particles are chosen in order to lead the other particles; in the second method, each existing particle follows the best solution found through iterations, and this is considered an advantage of evolutionary calculation methods. Because PSO is working simply simpler and is more efficient, it is used in clinical centers and for other medical applications like branch cut level unwrapping of MRI data (22) and tumor categorization.

In this current article, a novel approach is presented which is based on the normalized normal constraint method (NNCM) using multi-objective mathematical programming (MOMP). The MOMP method has the ability to properly manage the merging of the dipped edges of the object. Furthermore, the suggested method solves the emerging problem of the duration of sorting the information of the database in the sequential CT and MR images of the human heart and human left ventricle. At last, in order to clarify the sequencing of CT classifications obtained by the MOMP model, we have provided a three-dimensional (3D) reshaping approach for the human heart.

We present the following article in accordance with the MDAR reporting checklist (available at http://dx.doi.org/10.21037/jtd-20-3339).

Methods

Proposed solution model

The NNMC method is defined as an MOMP method that divides the objective space into possible and impossible spaces (20), using the best Pareto solutions. The objective space and solution space are different concepts entirely, with the objective space referring to a vector space that is composed of objective functions of the MOMP issue and its proportions. The obtained mean of NNCM has demonstrated its capability to provide the best Pareto solution and distribute it evenly across the Pareto set (21). If there will not be any loss, the flowing ϵψ formula is used in order to calculate the amount of generic MOMP issues:

$$AMa{x}_{zϵ\psi }MC\left\{f1\left(z\right),\dots ,f_i\left(z\right),\dots ,f_k\left(z\right)\right\}$$[1]

The following stages demonstrate the functions of NNCM in order to solve the MOMP issue in Set 1 above:

Stage 1 computes the best value of the I^th objective performance, such as $F_i^{op}\left(Z_i^{op}\right)=ma{x}_{Z\in \psi }MC F_i\left(Z\right) \forall i \in \left\{1,2,\dots ,k\right\}$, by calculating the value of k separately in a single objective optimization issue. After this, the assigned vector $Z_m^{op}$ is placed in the objective function of k-1, in order to achieve an anchor point of the i^th in the objective function of A_i; the quantity of F_m is then computed as follows: $\left({\text{z}}_{\text{i}}{}^{\text{op}}\right)\forall \text{m}\in \left\{\text{1, }\cdots \text{, I-1, i+1, }\cdots \text{, k}\right\}$.

Stage 2: the matrix ∆ of payoff is made via placing the anchor points A_i in the column array in the following manner:

$$\Delta \triangleq \left[\begin{array}{c}{A}_1\\ ⋮\\ A_i\\ ⋮\\ A_k\end{array}\right]=\left[\begin{array}{ccccc}{F}_1^{op}\left(Z_1^{op}\right)& \cdots & F_i\left(Z_1^{op}\right)& \dots & F_k\left(Z_1^{op}\right)\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ F_1\left(Z_i^{op}\right)& \dots & F_i^{op}\left(Z_i^{op}\right)& \dots & F_k\left(Z_i^{op}\right)\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ F_1\left(Z_k^{op}\right)& \cdots & F_i\left(Z_k^{op}\right)& \dots & F_k^{op}\left(Z_k^{op}\right)\end{array}\right]$$[2]

Overall, while an objective performance of an MOMP issue can be solved separately, a possibility exists that most of the decision variables of vector Z are not assigned by a single objective optimization. In order to solve this problem, the remaining unassigned decision variables may be assigned by lexicographic optimization (20). However, in the proposed multi-objective information-gap decision theory-distribution network reinforcement planning (IGDT-DNRP) model, all decision variables (e.g., the decision variables of investment a_it and ᵝ_ijt and decision variables of operation such as GP_itl and LS_itl) are unproblematically determined by single objective optimization of the objective function separately.

Stage 3: to prevent the masking effect of objective performances lying in different rages, all the objective performances of MOMP should be normalized, based on the payoff matrix obtained in Stage 2, using the following equation:

$$F_i^n\left(Z\right)=\left[\raisebox{1ex}{$\left(F_i\left(Z\right)-F_i^{ws}\left(Z_i^{op}\right)\right)$}\!\left/ \!\raisebox{-1ex}{$\left(F_i^{op}\left(Z_i^{op}\right)-F_i^{ws}\left(Z_i^{op}\right)\right)$}\right.\right] \forall i \in \left\{1,2,\dots ,k\right\}$$[3]

In the above equation $F_i^{op}\left(Z_i^{op}\right)$ and $F_i^{ws}\left(Z_i^{op}\right)$ show the best and the worst quantity of the i^th column in the payoff matrix, respectively, and n stands for the normalized value.

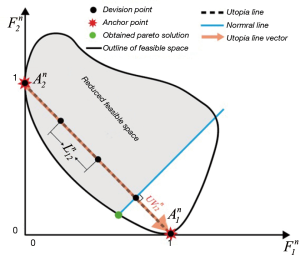
Stage 4: through attaching all anchor points of A_i, a lower subspace of the objective space, named the utopia hyper plane, can be made. In the example of bi-objective issues (k=2), as shown in Figure 1 (bt dotted black line), the utopia hyper plane it is called the utopia line, as all hyper planes in the two-dimensional (2D) vector space are considered lines.

Stage 5: a hyper plane of the normalized utopia vectors taken from $U{V}_{ik}^n$ is created by attaching to $A_i^n$ to $A_k^n\forall i \in \left\{1,\cdots ,k-1\right\}$, according to the following formula:

$$U{V}_{ik}^n= A_k^n- A_i^n$$[4]

It should be noted that the utopia hyper plane vectors for the bi-objective issues are named utopia lines, as shown in Figure 1 by the brown arrows. In the Figure 1, $A_i^n$ and $A_2^n$ are shown by red stars and represent two standardized anchor points in the generic bi-objective issues.

Stage 6: the standardized increase of $U{V}_{ik}^n$ is calculated using $L_{ik}^n\forall i\in \left\{1,\cdots ,k-1\right\}$ with the following equation:

$$L_{ik}^n=\Vert U{V}_{ik}^n\Vert /\left(S{P}_{ik}-1\right)$$[5]

In the above equation, $S{P}_{{}_{ik}}\forall i \in \left\{1,\cdots ,k-1\right\}$ are the predetermined set points and indicate the number of division points of $U{V}_{ik}^n$; they evenly allocate the division points on $U{V}_{{}_{i }}^{kn}\forall i \in \left\{1,\cdots ,k-1\right\}$, and all the set points of $S{P}_{ik }\forall i \in \left\{1,2,\cdots ,k-1\right\}$ must be connected to each other according to the following equation:

$$S{P}_{ik}=\left(S{P}_{1k}.\Vert U{V}_{ik}^n\Vert \right)/\Vert U{V}_{1k}^n\Vert$$[6]

Based on Eq. [6], the number of division points that include $U{V}_{ik}^n$ depends on the Euclidian model of $\Vert U{V}_{1k}^n\Vert$, and SP_1k as a pre assigned set point. Figure 1 shows the normalized increase of $L_{iki}^n$ which creates a bi-objective issue, represented by $L_{12}^n$.

Stage 7: the j^th utopia points of the hyper plane are connected as shown by D_j on the utopia hyper plane on the basis of the weighted linear mix of standardized anchor points based on the following equations:

$$D_j={\displaystyle \sum {}_{\forall i\in \left\{1,2,\cdots , k\right\}}}{\omega }_{ji}.A_i^n$$[7]

When

$$0\le {\omega }_{ji}\le 1$$[8]

$${\displaystyle \sum {}_{\forall i\in \left\{1,2,\cdots , k\right\}}}{\omega }_{ji}=1$$[9]

In order to extend each of the D_j points, the quantities of each point should be altered regularly within the range of [0, 1] by using the stage of $\frac{1}{SP-1}$^{. For example, in the bi-}objective MOMP issue with k=2, there are two extra anchor points which belong to objective performances. In this method of calculation, with the quantity of SP postulated as SP _ik=5, the range of obtained values of ω_ij through Eqs. [8] and [9] can be determined as follows:

$$\left({\omega }_{j1},{\omega }_{JZ}\right)\text{=}\left\{\left(0,1\right),\left(0.25,0.75\right),\left(0.5,0.5\right),\left(0.75,0.25\right),\left(1,0\right)\right\}$$[10]

Looking at Eq. [10], it can be seen that the five drawn division points (or five utopia points of the hyper plane) can be generated through creating the mechanism of Eqs. [7] and [9]. The black circles in Figure 1 represent the same distribution of spaced utopia points of the hyper plane or division points for the bi-objective issues.

Figure 1 Standardized objective space for the a bi-objective MOMP issue. MOMP, multi-objective mathematical programming.

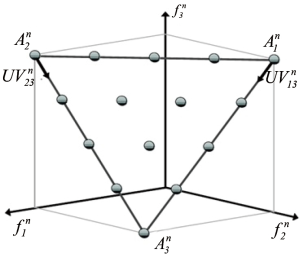
In order to demonstrate the function of the produced mechanism of the utopia points of the hyper planes, the weighting parameters of ω_ji are generated through using the three objective MOMP problems with k=3, as is shown in Figure 2 (the quantity of SP_ik =5 is postulated). Figure 2 illustrates that the 15 utopia points with the values of ω_ji will be the following:

Figure 2 Generated values for a three-objective MOMP problem. MOMP, multi-objective mathematical programming.

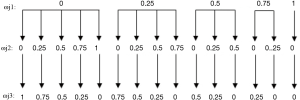
(ω_j1, ω_jz, ω_j3) = {(0, 0.1), (0, 0.25, 0.75), (0, 0.5, 0.5), 0, 0.75, 0.25), (0, 1.0), (0.25, 0, 0.75), (0.25, 0.25, 0.5), (0.25, 0.5, 0.25), 0.25, 0.75, 0) (0.5, 0, 0.5), (0.5, 0.25, 0.25), (0.5, 0.5, 0), (0.75, 0, 0.25), (0.75, 0.25, 0), (1, 0, 0)}

These 15 utopia points of the hyper plane in the standardized objective with the synchronization of $F_{{}^1}^n$, $F_{{}^2}^n$, and $F_{{}^3}^n$ are illustrated in Figure 3. Figure 3 also shows the three anchor points of $A_{{}^1}^n$, $A_{{}^2}^n$ and $A_{{}^3}^n$ beside the two utopia hyper plane of vectors of $U{V}_{13}^n$ and $U{V}_{23}^n$_.Figure 3 depicts the even distribution of utopia points of the hyper plane in the standardized objective space, which is a benefit of the NNCM approach to solve the above-mentioned problem

Figure 3 Standardized objective space for a three-objective MOMP issue showing the utopia hyper plane points. MOMP, multi-objective mathematical programming.

Steps 8: a Pareto solution is generated for D_j by calculating the under single objective optimization issue as follows:

$$\underset{Z\in {\psi }^{MC}}{\max }{F}_k\left(Z\right)$$[11]

$$\left(F^n-D_j,U{V}_{ik}^n\right)\le 0i=1,2,\cdots ,k-1$$[12]

In which the (0, 0) shows the inner division between two vector points of view.

In addition, ${\text{F}}^{\text{n}}\text{= }\left({\text{F}}_1^{\text{n}}{\text{ (z), F}}_2^n\text{ (z),}\cdots {\text{,F}}_k^n\text{ (z)}\right)$ is one of the points in the k-dimensional standardized objective space. The limits of Eq. [12] are added to the basic limits of Z =ϵψ^MC of the MOMP issue. According to Eq. [12], the possible section of the objective space is lowered to a subspace which is covered through the ordinary hyper planes, in a way that the ordinary hyper plane is specified to a special utopia of the hyper plane in the vector $U{V}_{ik}^n$. The ordinary hyper line in k=2 is named the normal line, which is specialized to a particular utopia line vector. Figure 1 illustrates the normal line which is drawn in blue. The gray lines in Figure 1 show the lowered possible local point for each division points, which is the division point of the blue and brown line vector. Correspondingly, in Figure 1, the achieved Pareto solution of division points are shown by green circles.

As mentioned, the MOMP issue of the IGDT-DNRP model, which is composed of five objective performances, can be computed by NNCM. Similarly, the limits in the solution space (e.g., ψ^MC) cover the above parts and limitations of the objective space which are presented here. In order to assign the optimal solution among the range of Pareto solutions, this search suggests a method based on the posterior o ut-of-sample analysis.

A posterior out-of-sample analysis

The current section proposes a posterior out-of-sample analysis in order to discover the optimal strengthening strategy and to extend the system based on the long operation function of each generated Pareto solution via a massive number of scenarios. We used Latin hypercube sampling (LHS) (21) to produce the posterior out-of-sample scenarios. By applying a Pareto optimal strengthening strategy, the following phases provided the proposed a posterior out-of-sample analysis:

Phase 1: the scenario counter begins with s=0. The variables of investment decision are fixed on the best quantities which are obtained through calculating the suggested MOMP IGDT-DNRP (e.g., ${\alpha }_{it=}{\alpha }_{it}^{op}$ and ${\beta }_{ijt=}{\beta }_{ijt}^{op}$). In this way, the mixed integer nonlinear programming (MINLP) issue of DNRP will be a non-linear programming (NLP) model because its two-fold, numerical variables are stable.

Phase 2: the number a posterior out-of-sample scenarios (for example NS) are elaborated.

Phase 3: the range of [0, 1] can be divided into K_e middle subintervals for all ambiguous variables which are in the suggested planning model (e.g., DP _itl, EP_tl, CR_ij, CC_i, and CO_itl)_, to create a random value for each subinterval.

Phase 4: the opposite cumulative distribution function (CDF) transformation of the K_e which is obtained from the random numbers for all ambiguous variables in Phase 3 can be computed. Consequently, there will be a range of K_e dissimilar comprehensions for all ambiguous variables.

Phase 5: S is adjusted to s + 1 in order to create a scenario vector for every ambiguous variable (for instance; $\widetilde{D{P}_{it1}},\widetilde{E{P}_{t1}},\widetilde{C{R}_{ij}}, \widetilde{C{C}_{\text{i}}},and \widetilde{C{O}_{it1}}$) through selecting a comprehension for all ambiguous variables which are obtained in Phase 4.

Phase 6: if the vector be is equal to one of the old previously generated scenario vectors 1…, eliminate the scenario vector is eliminated, and then back to the procedure returns to Phase 5; otherwise, go to Phase 7 step can begin 7.

Phase 7: $\widetilde{D{P}_{it1}},\widetilde{E{P}_{t1}},\widetilde{C{R}_{ij}},\widetilde{C{C}_i},and\widetilde{C{O}_{it1}}$ is changed which inclines towards the scenario vectors in the NLP optimization problem of Phase 1. The issues of subsequent NLP optimization are removed to be in the shape of the proposed optimization problem according to the decision variables of GP_itl and LS_itl, in order to discover the direct thrust control (DTC) for each scenario vector of s (for example; DTC_s).

Phase 8: in the condition of s < NS, Phase 5 is repeated; otherwise, ETC is calculated as follows: $ETC=\frac{{{\displaystyle \sum }}_{s=1}^{NS}DTCs}{NS}$.

The presented posterior out-of-sample analysis can be operated for every Pareto optimal solution with the aim of discovering the optimal strengthening strategy with the least quantity of ETC.

The suggested images of the segmentation method

The suggested MOMP is driven from the PSO, and the section below, proposed approach, describes the ACM. Moreover, a range of related metrics for assessing the function of the suggested model is provided in the Validation metrics section Validation metrics.

Proposed approach

In order to avoid the two basic disadvantages of traditional ACM, the proposed MOMP can be used to trigger multiple active contours which are categorized in terms of the object of interest based on the emerging problems of polar optimization process. As the model of the suggested MACPSO makes it easy to apply the classical implementation of PSO, some benefits are inherently acquired, such as robustness, low computational time, and efficiency. Figure 1 shows the suggested segmentation method, which is described below.

In the initial step of processing of MOMP model, the noises of image are removed by using a 2D median filter (3×3 window size). As a result, in order to determine the distance between the background and locals of interest, the Canny age is applied. In the last step of this procedure, the Euclidean distance map is generated in order to minimize the procedure. In the second step of MOMP initialization on the resulting distance map, the origin point of cooperating network can be determined by the user in a collaborative manner. The produced coordination network classifies the locals of interests by using the equation, $\theta =2\frac{\pi }{g}$ in which g stands for the degrees of every of limited polar part of S. Conversely, the circular and elliptical forms based on the frame of local of interest makes the N initial contour number, and considered the region of interest is considered to be placed inside the spatial domain. Then, after presenting the N counter, the process generates the N snaxel control points and consequently detects the particles of all of the limited polar section S_i. Also, in the above equation, the edge sectional solution and swarm of particles, which is shown by O_I, should be present. In all sections of S_i, the proposed strategy is used in order to properly conduct a segmentation procedure, and consequently, the optimization problem is placed into the appropriate age sectional solution.

Compared to other methods, our proposed method has three marked benefits in the operation procedure. The first benefit is that the beginning contours can be mechanically started in the circular or elliptical arrangements. The second benefit is that the modified number of sections can easily and directly modify the number of snaxels and then classify the objects of interest. In order to use this method correctly, the algorithm parameters should be carefully measured and based on the form of the object of interest in order to achieve a precise segmentation without accepting the function of the proposed model.

The third benefit is that the basis or primary point is created by users, and can be used to promptly produce all the snaxels based on the spatial domain and object of interest. Furthermore, the proposed method can easily outspread the classification of sequential CT and MR images simply through recreating the basic points by placing the set of images appropriately.

The following summarizes the process of the suggested MOMP image classification method:

• The basic point, degrees of G, and the numbers of selected snakes are harmonized by operation point.
• The numbers of iteration, inertia weight, and learning factors are the operation parameters of the proposed algorithm.
• For each polar section of S_i, only one swarm is produced while the existing snaxels are detected.
• The operation of parameters and detection of the beginning points for each decision variable are then completed.

Validation metrics

The metrics of the Jaccard index, Dice index, the Hausdorff distance, and area perimeter were used to evaluate the ability of the proposed method to classify medical images in comparison to the traditional ACM and gGraph cut method.

The Jaccard index J (A, B) as shown in Eq. [13], and the Dice index D (A, B), as shown in Eq. [14], are between [0, 1], and were applied to the binary variables (4). The mentioned indexes were computed by Eqs. [13] and [14]. In this method, a represents the classified regions calculated by mathematical models (MOMP and the traditional dynamic contour model) and B represents the regions determined by experts. Under the two above-mentioned indexes, the outcome was 1 and 0 if the regions of A and B overlay each other; otherwise the following formula was used:

$$J\left(A,B\right)=\frac{A\cap B}{A \cup B }$$[13]

$$D\left(A,B\right)=\frac{2\left(A\cap B\right)}{A=B}$$[14]

In order to match the shapes in the medical image classification, the Hausdorff distance index was used. It calculates the similarity in the two provided sets, where, “a” and “b” are determined in the A and B sets, and $\Vert a-b\Vert$ are considered to be the Euclidean distance:

$$H(A,B)=\underset{a\in A}{{\displaystyle \max }}\underset{b\in B}{{\displaystyle \min }}\Vert a-b\Vert$$[15]

The results section details the classification outcomes of synthetic and medical images by applying the proposed MOMP method and summarizes the analysis of the validation metrics.

We assessed the function of the proposed MOMP method to classify the objects of interest and unreal images. In the present study, the calculations were completed using the GNU Compiler Collection version 4.4.5 which was operated in Debian GNU/linux 6. 0, Intel Core I3 with 2.13 Ghz and Gb of memory.

Results

Use of synthetic images

Evaluation of the quality of classified objects by using the MOMP method in the three distinct balanced test images showed that, in comparison to the traditional applications of ACM, our proposed method is more consistent and precise. The algorithm process which is conducted by particles of swarm optimization makes the MOMP method more strong, while the traditional ACM does not have this benefit. Furthermore, the results also indicated that the proposed method can overcome the local minimum points of objective functions, which the other models (such as ACM) are find the local minima points. These results suggest the performance of the proposed model is superior to that of the other methods.

Usage of medical images

The proposed method was able to organize sequential CT and MR images related to the human heart and human left ventricle. These medical images were provided by the Mexican Social Security Institute and the Auckland MRI Research Group from University of Auckland.

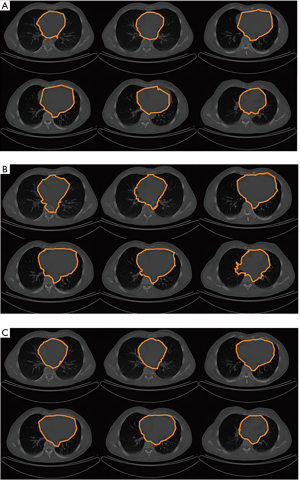
A CT scan, 512×512 pixels in size, taken for the classification of the human heart is illustrated in Figure 4. Figure 5A is the test photo and Figure 5B shows the outline of the human heart by cardiologists. Moreover, the regions classified by the ACM model with42 control points, $\propto \text{=}0.01$, β=0.9, and γ=0.05(in 0.087s), are shown in Figure 5C. According to Figure 5D, the classification of the human heart through using the proposed MOMP method is placed precisely in the boundaries of the human heart. The parameters used in the classification are estimated as iteration =0, inertia weight =0.8, learning factor =0.5, number of snakes =15, quantity of g =5 (with 42 snaxels in each snake), and administration time =0.127 s.

Figure 4 The process of the proposed method’s MOMP image classification method. (I) In order to remove inappropriate decision variables, limited research space is used. (II) All decision variables in the fitness performance are accessed. (III) The new version of the decision variables is used to adjust for better decision variables. (IV) The algorithm loop is then repeated. (V) The process is continued until a satisfying number of iterations is obtained. MOMP, multi-objective mathematical programming.

Figure 5 CT images. (A) Test photo; (B) the human heart as visualized by experts; (C) outcomes of classical ACM; (D) outcomes of the proposed MOMP method. CT, computed tomography; ACM, active contour model; MOMP, multi-objective mathematical programming.

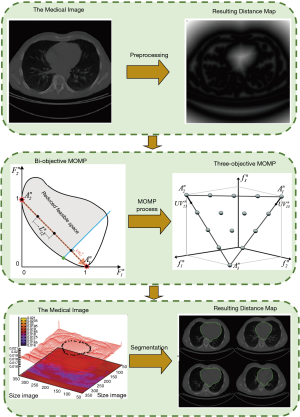
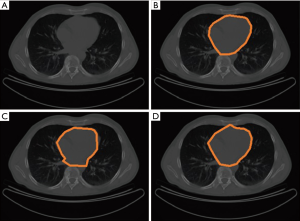
Figure 6 demonstrates the procedure of the convergence of the MOMP method with the CT test photo. In this figure the proposed algorithm is compared with two other optimization model i.e., genetic algorithm (GA) and ant colony (ACO). As shown in this figure, the proposed algorithm provides better convergence speed (20 iteration) with better accuracy in comparison with two other models of GA and ACO. The assessment of convergence is conducted using the fitness value to calculate the mean of monitoring points on the surface of space potential with its size being decreased by the 20 predetermined iteration numbers in order to enhance the classification of the human heart.

Figure 6 Convergence comparison of human heart classification by the proposed model with genetic algorithm and ant colony algorithm through CT images, CT, computed tomography.

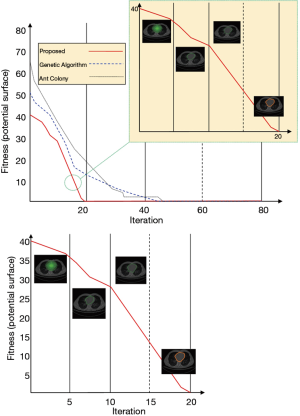
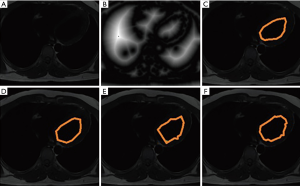
Figure 7 is a comparison of medical images, 512×512 pixels in size, obtained from the MRI scan with the purpose of classifying the human left ventricle. Figure 7B provides a map of the Euclidean space taken from the test images in order to increase the understanding of the classification process. Figure 7C,D shows the human left ventricle visualized by two experts. Figure 7E illustrates the obtained outcomes of the segmentation result by use of traditional ACM with the following parameters: $\propto \text{=}0.01$, β=0.9, and γ=0.05 (in 0.085s). Figure 7F shows the obtained outcomes of classification by the proposed MOMP method which accurately detected the boundaries in the left ventricle. The quantities of the mentioned parameters are determined as follows: iteration =20, inertia weight =0.8, learning factor =0.5, numbers of snakes =9, quantity of g =15 (with 42 obtained snaxels per snake), and administration time =0.102 s.

Figure 7 MRI scans. (A) Test image; (B) Euclidean space map of test images; (C) the human left ventricle as outlined by expert 1; (D) human left ventricle as outlined by expert 2; (E) outcomes of traditional ACM; (F) outcomes of MOMP. MRI, magnetic resonance imaging; ACM, active contour model; MOMP, multi-objective mathematical programming.

The procedure of segmentation of the MOMP method with the MR images was completed by calculating the mean of the monitoring points rather than fitness value on the surface of space potential for each iteration. The convergence was completed using the same parameters as those displayed Figure 7.

By virtue of how the MOMP method is conducted, it has the ability to operate with the sequential image data sets simply by creating the connected x and y coordinates in the original points and initial parameters in the total image collection (Figure 8). The operation procedure is clearly superior to that of traditional ACM, as it requires only one user to generate the snaxels for the classification procedure, while in the traditional ACM method, snaxels should be presented interactively, with more time being needed compared to the proposed method.

Figure 8 The convergence of human left ventricle classification by PSO iteration with MRI. PSO, particle swarm optimization; MRI, magnetic resonance imaging.

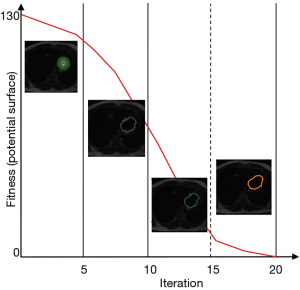
Figure 9 shows outcomes obtained from the classification of a subset of CT image of the human heart. The images are gathered from datasets which include 144 sequential CT images of different patients, 512×512 pixels in size. The outcomes obtained from classification by the interactive graph cut method are shown in Figure 9B, and were calculated in 10.065 s. In the MOMP method, the areas determined by experts (the human heart and background seeds) must be kept apart from the classification process. Figure 9C shows the images classified by applying the MOMP method appropriately in the boundary of the human heart. In the above simulation, the parameters of the suggested method were as follows: iteration =20, inertia weight =0.8, learning factor =0.5, number of snakes =15, quantity of g =15 (with 42 snaxel per snake), and administration time = of 11.152 s. Table 1 lists the outcomes obtained from classification by two experts, traditional ACM, graph cut, and the MOMP method, from the CT image datasets mentioned above. The results from Figure 9 show that the MOMP method is more precise and accurate in the classification of the human heart.

Figure 9 CT photos of human heart segmentation. (A) Outcomes of traditional ACM; (B) outcomes of the graph cut method; (C) outcomes of MOMP usage. CT, computed tomography; ACM, active contour model; MOMP, multi-objective mathematical programming.

Table 1 The Jaccard index, the Dice index, and the Hausdorff distance evaluated the average similarity among the segmented regions by traditional ACM, the graph cut, and proposed (MOMP) methods, along with regions outlined by two experts in the range of CT images
Full table

Figure 10 summarizes the results of segmentation of MR images of the human left ventricle. These images were collected from a database of 23 sequential MR images, each 512×512 pixels in size. Figure 10 demonstrates the obtained outcomes of classification by using the traditional ACM, in which the outcomes of snake movement could not fine-tune themselves with the ventricle boundaries. The following parameters of ACM were determined under an administration time of 4.183 s and a control point of 42: $\propto \text{=}0.01$, β=0.9, and γ=0.5. In order to implement the graph cut model, the experts defined the human left ventricle and related kernels. Figure 10B shows the classification outcomes which were obtained from the interactive graph cut method using an administration time of 3.726 s. Figure 10C shows the images produced by the MOMP method, which clearly determined the boundaries of the human left ventricle. In the simulation conducted, the selected parameters of the proposed MOMP method were determined as follows: iteration =20, inertia weight =0.8, learning factor =0.5, number of snakes =9, quantity of g =15 (with 42 snaxels per snake), and administration time =5.179 s.

Figure 10 MRI of human left ventricle segmentation. (A) Outcomes of traditional ACM; (B) outcomes of the graph cut method; (C) outcomes of MOMP. MRI, magnetic resonance imaging; ACM, active contour model; MOMP, multi-objective mathematical programming.

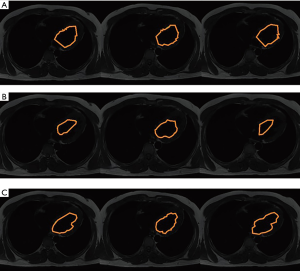
Furthermore, in order to evaluate the outcomes obtained from the classification of the data set in the above-mentioned sequential MR images, the required comparative outcomes from the Hausdorff distance, Jaccard index, and the Dice index were analyzed and are listed in Table 2. The analysis of similarities between the traditional method and proposed method showed that the proposed method is set properly and capably performed segmentation of the left ventricle. Table 3 shows a comparison of the region and boundary performances of the proposed method, traditional ACM, graph cut, and experts.

Table 2 The Jaccard index, the Dice index, and the Hausdorff distance evaluated the average similarity among the segmented regions using traditional ACM, graph cut method, and proposed (MOMP) methods, along with regions outlined by two experts in the range of CT images
Full table

Table 3 Average selected area and perimeter of the determined pixels achieved by traditional ACM, graph cut, and the MOMP methods, along with regions outlined by two experts with a range of CT and MR images
Full table

As can be seen in Table 1, outcomes obtained from the comparison with expert segmentation, evaluation of distance, and similarities confirm that the proposed MOMP method works well in the segmentation of the human heart when using CT images, and corresponds with the obtained accuracy numbers (92% and 97%, respectively, as calculated by expert 2) of the Jaccard and Dice indexes. Also, as can be seen, the Hausdorff distance of the proposed method is lower than that of the ACM and graph cut methods. In addition, Table 2 shows that the accuracy of the proposed method in lower contrast and noise conditions of MRI images is 87%, which is in an acceptable range

Also, the outcomes obtained from the elected area and perimeter evaluations illustrate that the MOMP method has high stability compared to the ACM and the graph cut method, as the quantities of the MOMP correspond with the experts’ outcomes.

As the proposed MOMP method performed well in segmenting the cardiac image sequence, it may have value in the 3D reconstruction of human organs. The Obtained results obtained in our experiment prove of the validity of the proposed approach.

Conclusions

In this study, we introduced a novel method for image photo segmentation on the basis of multiple active contours taken from MOMP. The proposed MOMP method divides the research area into polar sections in order to remove or at least decrease the amount of sensitivity towards the primary contour position and reduce the disadvantages caused by region minima in traditional active ACM. The ability of our method was first tested via comparison with traditional ACM using synthetic images derived from medical cardiac CT and MRI images. The outcomes from these experiments indicate that our proposed method performs well in the presence of noise and concavities in comparison to the traditional ACM.

By virtue of its superior performance, the proposed method better performance may have value in precise human heart and human left ventricle segmentation as compared to segmentation performed by experts and the graph cut method, as evidenced by likelihood metrics. Furthermore, the findings demonstrated that the regional application of polar sections by stable factors in the MOMP method is applicable to medical images, and can dissect the datasets of successive medical images within a convenient operation time.

Acknowledgments

Funding: None.

Footnote

Reporting Checklist: The authors have completed the MDAR reporting checklist. Available at http://dx.doi.org/10.21037/jtd-20-3339

Data Sharing Statement: Available at http://dx.doi.org/10.21037/jtd-20-3339

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/jtd-20-3339). The authors have no conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Castillejos H, Ponomaryov V, Nino-de-Rivera L, et al. Wavelet transform fuzzy algorithms for dermoscopic image segmentation. Comput Math Methods Med 2012;2012:578721. [Crossref] [PubMed]
2. Davuluri P, Wu J, Tang Y, et al. Hemorrhage detection and segmentation in traumatic pelvic injuries. Comput Math Methods Med 2012;2012:898430. [Crossref] [PubMed]
3. Nyma A, Kang M, Kwon YK, et al. A hybrid technique for medical image segmentation. J Biomed Biotechnol 2012;2012:830252. [Crossref] [PubMed]
4. Hsu WY. Improved watershed transform for tumor segmentation: Application to mammogram image compression. Expert Systems with Applications 2012;39:3950-5. [Crossref]
5. Cuevas E, Osuna-Enciso V, Zaldivar D, et al. Multithreshold Segmentation Based on Artificial Immune Systems. Mathematical Problems in Engineering 2012;2012. [Crossref]
6. Boykov Y, Jolly MP. Interactive Organ Segmentation Using Graph Cuts. In: Delp SL, DiGoia AM, Jaramaz B. editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2000. MICCAI 2000. Lecture Notes in Computer Science, vol 1935. Springer, Berlin, Heidelberg, 2000:276-86.
7. Schmidt FR, Toppe E, Cremers D. Efficient planar graph cuts with applications in Computer Vision. IEEE Computer Society Conference on Computer Vision and Pattern Recognition 2009, Miami, Florida, 2009:351-6.
8. Chen DR, Chang RF, Wu WJ, et al. 3-D breast ultrasound segmentation using active contour model. Ultrasound Med Biol 2003;29:1017-26. [Crossref] [PubMed]
9. Gao L, Liu X, Chen W. Phase- and GVF-Based Level Set Segmentation of Ultrasonic Breast Tumors. Journal of Applied Mathematics 2012;2012:810805. [Crossref]
10. Liu X, Haider MA, Yetik IS. Unsupervised 3D Prostate Segmentation Based on Diffusion-Weighted Imaging MRI Using Active Contour Models with a Shape Prior. J Electrical and Computer Engineering 2011;2011:410912. [Crossref]
11. Zhu X, Zhang P, Shao J, et al. A snake-based method for segmentation of intravascular ultrasound images and its in vivo validation. Ultrasonics 2011;51:181-9. [Crossref] [PubMed]
12. Dagher I, Tom KE. WaterBalloons: A hybrid watershed Balloon Snake segmentation. Image and Vision Computing 2008;26:905-12. [Crossref]
13. Wang L, He L, Mishra A, et al. Active contours driven by local Gaussian distribution fitting energy. Signal Processing 2009;89:2435-47. [Crossref]
14. Amjady N, Abedinia O. Short Term Wind Power Prediction Based on Improved Kriging Interpolation, Empirical Mode Decomposition, and Closed-Loop Forecasting Engine. Sustainability 2017;9:2104. [Crossref]
15. Shayanfar H, Shayeghi H, Abedinia O, et al. Design Rule-Base of Fuzzy Controller in Multimachine Power System Stabilizer Using Genetic Algorithm. 2010.
16. Abedinia O, Amjady N, Kiani K, et al. Multiobjective environmental and economic dispatch using imperialist competitive algorithm. ARI - An International Journal for Physical and Engineering Sciences 2012;4.
17. Izadfar HR, Shayanfar H, Amjady N, et al. Multi-machine power system oscillation damping: Placement and tuning PSS VIA multi-objective HBMO. Int J Birth Parent Educ 2012;4:1-8.
18. Abedinia O, Ghasemi A, Ojaroudi Parchin N. Improved time varying inertia weight PSO for solved economic load dispatch with subsidies and wind power effects. Complexity 2014.21.
19. Abedinia O, Salay Naderi M, Jalili A, et al. A Novel Hybrid GA-PSO Technique for Optimal Tuning of Fuzzy Controller to Improve Multi-machine Power System Stability. International Review of Electrical Engineering 2011;6:863-73. (IREE).
20. Ghasemi A, Abedinia O, Shayanfar H, et al. PSO-TVAC algorithm for multi objective PSS design in multi-machine power system. 2011.
21. Abedinia O, Amjady N, Salay Naderi M. Optimal congestion management in an electricity market using Modified Invasive Weed Optimization. 2012 11th International Conference on Environment and Electrical Engineering, EEEIC 2012 - Conference Proceedings 2012.
22. Ghadimi N, Akbarimajd A, Shayeghi H, et al. Application of New Hybrid Forecast Engine with Feature Selection Algorithm in Power System. International Journal of Ambient Energy 2019;40:494-503. [Crossref]

(English Language Editor: J. Gray)