An overview of the use of artificial neural networks in lung cancer research
Introduction
The artificial neural networks (ANNs) are statistical models where the mathematical structure reproduces the biological organisation of neural cells simulating the learning dynamics of the brain (1). Although definitions of the term ANN could vary, the term usually refers to a neural network used for non-linear statistical data modelling. ANNs are based loosely on the hierarchical synaptic organisation of neurons in the brain and like a neuron that receives multiple inputs, they assign each input an importance (weight), and decides whether to fire depending on the summation of these weighted data. In broad terms, an ANN is usually composed of at least three layers made up of logical units (perceptrons). The input layer receives a data set (related to the research question). One or more hidden layers (connected in a specified hierarchical manner) synthesise this data. The output layer both receives the hidden layer(s) and generates the answer to the research question (2).
General properties of ANNs
ANNs have unique properties including robust performance in dealing with noisy or incomplete input patterns, high fault tolerance, and the ability to generalise from the training data (2). There have been numerous applications of ANNs within medical decision-making, and ANNs are beginning to feature regularly in medical journals, as evidenced by the numerous published papers each year featuring neural network applications in medicine. The advantage of ANNs over conventional programming lies in their ability to solve problems that do not have an algorithmic solution, or the available solution is too complex to be found. The ANNs can fulfil the statistical analyses that contain linear, logistic and nonlinear regression. Nevertheless, it is hard for ANNs to understand the structure of the algorithm. ANNs are a “black-box” technology and hence, they can hardly discover how to operate the classification (3). On the other hand, ANN models have several advantages over statistical methods. They can rapidly recognise linear patterns, non-linear patterns with threshold impacts, categorical, step-wise linear, or even contingency effects. Analyses by ANN need not start with a hypothesis or a priori identification of potentially key variables, so potential prognostic factors can be determined if they already exist in the masses of datasets, though they might have been overlooked in the past (4).
ANN functioning, potentialities and care of use
As well known, the first development of ANNs has been clearly inspired by neuroscience. However, as a matter of fact, the neural models applied today in various fields of medicine, such as oncology, do not aim to be biologically realistic in detail but just efficient models for nonlinear regression or classification. In this section, leaving a complete introduction of ANN to more key texts (5,6), a brief sketch of their structure, functioning and correct use will be presented. Further details and a more formal treatment can be found in a recent paper (7), where feedforward ANNs with backpropagation training (the networks which are almost exclusively used in oncological literature) are widely discussed, especially regarding their application to small datasets such as the typical ones encountered in medical sciences.
The structure of a feedforward network is presented in Figure 1. This kind of network is used for finding a fully nonlinear relationship between some variables in input and one or more variables in output. For instance, we may search for a quantitative link between variables that are supposed to be causally related (causes in input and effects in output). To do so, the network connects several layers of computational units (neurons) and calculates the outputs as composite functions of inputs. These features are highly nonlinear (the neurons transfer the weighted sum coming from the neurons of the previous layer through a sigmoid or a hyperbolic tangent to the neurons of the following layer) and critically depend on the values of weights (coefficients) associated with connections.
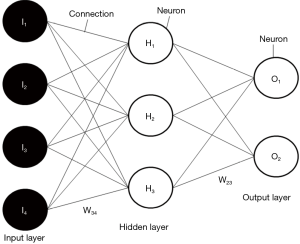
As in the standard linear regression we must find the coefficients related to the independent variables that can minimize the distance between the regression line and the experimental points to be linearly interpolated, here we should fix these weights to find a relationship that reduces the distance between the outputs of the network and the targets, the real (experimental or observational) values of the output variables. This can be obtained by training the network on known input-target pairs, with the final aim to find a general “law” that can correctly link the same input and output variables also for further unknown data samples. If this happens, it can say that the network “learned” from known data.
In short, we would like to achieve a good generalisation ability from an ANN model. But here a problem arises: ANNs are so compelling that, if many neurons in the hidden layers are allowed, they can correctly reconstruct the link between inputs and targets on a known dataset. In this case, however, ANNs overfit the data available and do not generalise well: if a new sample of data is presented to the network, the found relationship is not able to correctly represent a “law” for the new data. This, also, happens for linear regressions: if you have n data on a Cartesian plane, it can always fit them faultlessly by a polynomial of degree n−1, but nobody may say that it represents a natural law. This overfitting problem is even heavier in the nonlinear “world” of ANNs.
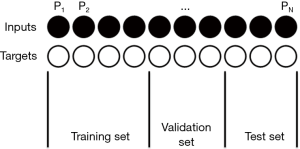
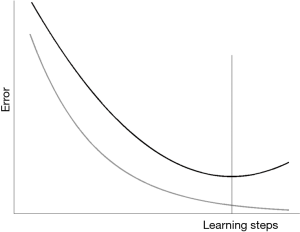
Thus, a first golden rule in using ANNs is to avoid overfitting. To obtain this result, one must be parsimonious and prefer small networks, for instance with a single hidden layer: it has been shown that one hidden layer is sufficient to approximate well any continuous function (8,9). Furthermore, the size of the networks must be related to the amount of data available for training. The number of ANN free parameters (connection weights) should be at least one order of magnitude less that the number of the input-target patterns, better if two order of magnitude less (10): otherwise, overfitting is “around the corner”. Finally, the convergence of the learning steps on the available data must not continue too much: this could lead the network to go too much close to the data themselves, so learning their specificities and not the general features of the links between inputs and targets. As better explained in a previous paper (7), for avoiding this last problem distinct samples should be chosen, one for training, one for validation and one for the test (Figure 2). The validation set can be used for deciding when stopping the training on the training set (for instance, when the ANN performance on the validation set begins to decrease) (Figure 3); another test set should be used for testing the performance of the relationship found on completely independent data, unknown to the network.
Contrary to what happens in a linear regression, when the achieved relationship is univocally determined by the function to be minimized (e.g., a squared function of distance between experimental points and the regression line), in the iterative training process of an ANN the result depends on the initial random choice of the connection weights, that, for instance, could not allow the network to find the absolute minimum of that function. There can be a substantial variability in the ANN outputs due to this initial choice, so that a good rule is to perform ensemble runs of the ANN model, each with different random initial weights, for either finding the best ANN or averaging and minimising this variability. Even the further variability due to a choice of the validation and test sets could be explored and eventually reduced by sorting different sets in various model runs.
Thus, the correct size and functioning of an ANN model are critical for obtaining reliable results. But even a proper understanding of the importance of input data and the interconnections among them is essential.
For instance, to consider small networks, we should choose just the most influential variables in input. But not always the inputs which are the most correlated with the output variables are those that allow the best performance of an ANN model. Here we are in a nonlinear landscape, and we should evaluate a nonlinear correlation for performing this choice (7). Furthermore, if two inputs are both highly correlated with the targets but they are also collinear between them, they give very similar information to ANN models, so that generally their joined use as inputs is almost not influential on the result or can even lead to a bad performance because this contributes to making the network larger and then more prone to overfitting. Finally, one could desire to understand the importance of the specific inputs for reconstructing the correct target in output. Again, the nonlinearity of the method does not permit to disentangle the skein in an easy way. Here a sum of causes (inputs) does not produce an amount of effects (outputs) as in a linear model: the only way to weight the importance of an input variable is to run the ANN model without that variable and to see how much the performance decreases. Higher is the decrease; higher is the impact of that input on the target reconstruction.
Brief assessment of ANN employ in literature
We have performed a review to assess the evidence for improvements in the use of ANN. It is accepted that the most reliable method of determining the effectiveness of a new intervention is to conduct a systematic comparative study with a randomised controlled trial (11). Nevertheless, we cannot perform a systematic review. Therefore, a search strategy using a combination of free-text words, relevant MeSH terms and appropriate filters was designed; the searching strategy was developed in EMBASE (via Ovid), MEDLINE (via PubMed) and Cochrane CENTRAL until the 01 April 2016, without imposing any language or time restrictions. Records identified through our search strategy were imported into reference management software. Letters, editorials, case reports, and reviews were excluded. We have selected ten papers about lung cancer used ANN in their methods (Table 1). Data extracted included study characteristics, baseline characteristics, study design, key results and statistical analysis.
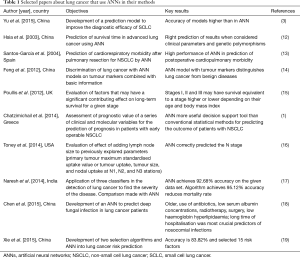
Full table
In the paper of Hsia et al. (12), the prediction of lung cancer outcome for determining further therapy survival time in advanced lung cancer was elaborated using ANN. ANN provides good prediction results when clinical parameters and genetic polymorphisms are considered in the model. The statistics setting was a feedforward ANN with architecture 25–4–1 for prediction of survival time and sensitivity analysis of the input variables. The analysis of results was performed through the rate of accuracy. From a statistical point of view, there was a risk of unreliable results due to overfitting, mainly caused by an over-dimensioned ANN (too many weights) on the small dataset available.
Santos-García et al. (13), in 515 patients underwent lobectomy or pneumonectomy for non-small cell lung cancer (NSCLC), designed a study with ANN to predict cardiorespiratory morbidity. ANN ensemble offered a high performance to predict postoperative morbidity. The statistics settings were a group of 100 feedforward ANN with architecture 13–20–1 or 13–30–1 for prediction of occurrence of cardiorespiratory morbidity after surgery. The analysis of results was performed through contingency table and ROC curve. There was a risk of unreliable results due to overfitting, mainly caused by over-dimensioned ANN (too many weights) on the limited dataset available.
In the paper of Feng et al. (14), realised an ANN model on the common tumour markers combined with essential information to predict lung cancer. The ANN model distinguishes lung cancer from benign lung disease and healthy people. Statistics was performed with a feedforward ANN with architecture 25–15–1 or 6–15–1 to discriminate between lung cancer and healthy or between lung cancer and other kinds of cancer. The analysis of results was performed with tables, sensitivity, specificity and accuracy. There was a risk of unreliable results due to overfitting, mainly caused by over-dimensioned ANN (too many weights) on the limited dataset available.
Poullis et al. (15) used the thoracic surgery database to evaluate factors other than the stage that can affect 5-year survival of lung cancer. Authors use a multivariate Cox regression model and ANN with two hidden layers (architecture 12–8–6–2) to predict long-term survival and to study the effect of age and body mass index on it. Even if the dataset is quite large, there is still a risk of unreliable results due to overfitting, caused by choice of an ANN with two hidden layers (the network has about 1,200 weights). Furthermore, no training-(validation)-test procedure seems to be adopted here for showing generalisation ability of the network.
In the paper of Toney et al. (16), the evaluation of the lymph node size added to three previous well studied parameters (primary tumour maximum standardised uptake value or tumour uptake, tumour size, and nodal uptake at N1, N2, and N3 stations) was realized with a feedforward ANN with architecture till to 8–8–4 and multiple cross-validations. Results were given regarding accuracy and ANN correctly predicted the N stage. Even if the multiple cross-validations can reduce the risk of unreliable results, overfitting may be present in this study because of the little numericity of the training set (67 patterns): often the networks used have more weights than training patterns.
Chatzimichail et al. (1) used the ANN to assess the prognostic value of a series of clinical and molecular variables in patients with early operable NSCLC. Authors found that ANN may represent a potentially more useful decision support tool than conventional statistical methods for predicting the outcome of patients with NSCLC and that some molecular markers enhance their predictive ability. They use a feedforward ANN with increasing inputs and decreasing hidden neurons for prediction of survival time and assessing the most important contribution factors. Results were given regarding judgment ratio and accuracy. Nevertheless, no details are provided for the number of hidden neurons in optimal networks, so that it is difficult to assess possible sources of overfitting. However, the adopted method of training, validation and test (on an entirely independent set) probably allows the authors to achieve reliable results.
In the paper of Naresh et al. (17), about the identification of lung cancer at an initial stage through three classifiers, the authors used the comparison with ANNs. Results were given regarding contingency tables, accuracy, precision, recall and specificity. No details were provided on the architecture of the networks so that it is difficult to assess this study. A simple training-test procedure was used, and this could lead to overestimation of ANN performance.
Chen et al. (18) develop an ANN to predict deep fungal infection in lung cancer. A feedforward ANN with architecture 9–7–1 was used. Analysis of results was made mainly through sensitivity, specificity and ROC curve. Basing on the described structure of the network, overfitting problems due to too many neurons (compared to the number of the clinical cases in the training sample) should be avoided. However, the simple training-test procedure (without validation) cannot assure a correct generalisation behaviour of the network and could lead to overestimation of ANN performance.
In the paper of Xiè et al. (19), about the exact relationship between risk factors and lung cancer, ANN predicted the lung cancer risk, Fisher and Relief-F algorithms and ANN were used for feature selection and prediction. Results were given regarding accuracy. No details were provided for the number of hidden neurons in optimal networks (endowed with 15 inputs) so that it was difficult to assess possible sources of overfitting. However, the K-fold cross-validation can reduce the risk of unreliable results, even if it cannot assure a correct generalisation behaviour of the network and could lead to overestimation of ANN performance.
Yu et al. (3) developed a prediction model to improve the diagnostic efficacy of small cell lung cancer. ANN was used as a benchmark. Results were presented regarding ROC curves. Even if no explicit details on the number of hidden neurons are supplied in the text, it can be deduced that this number is small; therefore, overfitting problems due to too many hidden neurons should be avoided. Nevertheless, the simple training-test procedure (without validation) cannot assure a correct generalisation behaviour of the network and could lead to overestimation of ANN performance.
Discussion
At least five papers (12-16) show sure signs of overfitting. This is due to the use of oversized networks that lead to having the same order of magnitude for the number of connection weights and the number of input target patterns in the training set: sometimes the first number even exceeds the second one! This leads to obtaining excellent results on the training set, due also to the fact that no early stopping through a validation set has been adopted in these papers. But, this way of acting does not permit to obtain a valid general rule for the searched relationship between inputs and outputs on unknown cases, so that the performances are not reliable. It is worthwhile to note that this problem is not understood and sometimes considered as a useful feature: in a paper (14), there is an even emphasis on the fact that “all the samples of training were determined correctly, the accuracy was 100%. The effect of fitting was perfect”.
In all the papers but one (1) the entire sets of data were divided just into training and test sets, without considering a validation set. In these cases, the presented results are the best ones obtained on the test set, but this means that the goodness of these results is overestimated because the authors aim to test the general validity of the found input-output relationships on the same set on which they have been tuned it. Sometimes a so-called K-fold cross-validation is used, in which the total round of data is divided into training and test sets with K different choices for the relative composition of the sets themselves. This way of acting can show if the ANN model can find stable relationships for various opportunities of training/test sets, but does not avoid the criticism previously cited about the overestimation of the ANN performances.
Apparently, the problems just discussed derive substantially from the non-availability of large datasets, so that an ANN tool for small datasets endowed with a correct learning algorithm could be beneficial. One needs to maximise the size of the training set without penalising the generalisation ability of the networks. It is worthwhile to note that a tool of this kind has been recently developed: it is summarised in a previous paper (7), used for the first time in climate change studies (20) and then applied to medical sciences, too (21).
The values of the weights fixed at the end of the learning algorithm also depend on the first random choices for them. This introduces a variability in the results of an ANN model that can be explored through ensemble runs, with the aim of identifying the best model, or minimising the variability itself and finding a more robust and stable average of the distinct ANN models. As a matter of fact, only one of the papers analysed here adopts this ensemble method (13).
As just seen, many problems arise from the too large networks considered. A way of minimising their architecture is to consider only the most influential variables as inputs, but seldom these are chosen with a preliminary statistical analysis in the papers analysed here. Sometimes they are chosen based on their linear correlation with the targets, but this is not sufficient in a nonlinear framework such that of medical sciences. Furthermore, some authors try to establish the most influential variables a posteriori, using some automatic tools of their ANN software, but even this method does not guarantee success. In fact, often these tools look at the magnitude of the weights which link a single input to the outputs, but the only method that guarantees to estimate the importance of one input on the reconstruction of a target correctly is that of pruning: run the ANN model with all the inputs but a particular input at a time and look at the network performances. Higher is the decrease of return; higher is the importance of the pruned input for reconstruction/prediction of the target.
There are many advantages and disadvantages in use of ANNs as classification and regression/prediction tools. ANNs have an excellent aptitude for learning the relationship between the input/output mapping from a given dataset without any prior information or assumptions about the statistical distribution of the data. This ability to learn from an individual dataset without any prior knowledge makes the ANNs suitable for classification and prediction tasks in clinical situations. Furthermore, ANNs are inherently nonlinear which makes them more useful for accurate modelling of complex data patterns, as opposed to others traditional methods based on extended techniques. Due to their behaviour, they have found application in a wide range of medical fields such as cardiology, gastroenterology, pulmonology, oncology, neurology, and paediatrics. One of the disadvantages of ANNs, when compared to logistic regression models, is that ANN frequently has difficulty analysing systems which have many inputs due to a significant amount of time taken to learn the system as well as possibly overfitting the model during the learning time. The linear and logistic regression models have less potential for overfitting mainly because the range of functions shaped is limited. Recently, the task of evaluation between these two models has been addressed from different aspects (1).
ANNs use a dynamic approach to analysing mortality risk, and their internal structure can be modified about a functional objective by bottom-up computation (the data are used to generate the model itself). Despite their powerlessness to deal with missing data, ANN models can simultaneously process numerous variables. ANNs can consider outliers and nonlinear interactions among variables. Therefore, whereas current statistics reveal parameters that are significant only for the overall population, the ANN model includes parameters that are important at the individual level, even if they are not significant in the overall population. Unlike standard statistical analysis, the ANN model can also manage complexity, even when samples are small and the ratio of variables to records unbalanced. In this respect, the ANN model avoids the dimensionality problem (2).
Conclusions
ANN inference has applications in tasks that require attention focusing. ANNs also have a niche to carve in clinical decision support, but their success depends crucially on better integration with clinical protocols, together with an awareness of the need to combine different paradigms in order to produce the simplest and most transparent overall reasoning structure, and the will to evaluate this in a real clinical environment (22).
Our analysis showed that often the use of ANN in the medical literature had not been performed in an accurate manner. This is detrimental for the reliability of the results presented. A strict cooperation between physician and biostatisticians could be helpful in determine and resolve the errors described.
Acknowledgements
The authors thank Stefano Amendola (Roma Tre University) for the helpful discussions.
Footnote
Conflicts of Interest: The authors have no conflicts of interest to declare.
References
- Chatzimichail E, Matthaios D, Bouros D, et al. γ -H2AX: A Novel Prognostic Marker in a Prognosis Prediction Model of Patients with Early Operable Non-Small Cell Lung Cancer. Int J Genomics 2014;2014:160236.
- Shi HY, Hwang SL, Lee KT, et al. In-hospital mortality after traumatic brain injury surgery: a nationwide population-based comparison of mortality predictors used in artificial neural network and logistic regression models. J Neurosurg 2013;118:746-52. [Crossref] [PubMed]
- Yu Z, Lu H, Si H, et al. A Highly Efficient Gene Expression Programming (GEP) Model for Auxiliary Diagnosis of Small Cell Lung Cancer. PLoS One 2015;10:e0125517. [Crossref] [PubMed]
- Zhou ZH, Jiang Y, Yang YB, et al. Lung cancer cell identification based on artificial neural network ensembles. Artif Intell Med 2002;24:25-36. [Crossref] [PubMed]
- Bishop CM. Neural networks for pattern recognition. Oxford: Oxford University Press; 1995.
- Hertz JA, Krogh AS, Palmer RG. Introduction to the theory of neural computation. Boulder: Westview Press; 1991: 327.
- Pasini A. Artificial neural networks for small dataset analysis. J Thorac Dis. 2015;7:953-60. [PubMed]
- Cybenko G. Approximation by superpositions of a sigmoidal function. Math Control Signals Systems 1989;2:303-14. [Crossref]
- Hornik K, Stinchcombe M, White H. Multilayer feedforward networks are universal approximators. Neural Networks 1989;2:359-66. [Crossref]
- Swingler K. Applying Neural Networks: A Practical Guide. Burlinton: Morgan Kaufmann; 1996.
- Jadad AR, Rennie D. The randomized controlled trial gets a middle-aged checkup. JAMA 1998;279:319-20. [Crossref] [PubMed]
- Hsia TC, Chiang HC, Chiang D, et al. Prediction of survival in surgical unresectable lung cancer by artificial neural networks including genetic polymorphisms and clinical parameters. J Clin Lab Anal 2003;17:229-34. [Crossref] [PubMed]
- Santos-García G, Varela G, Novoa N, et al. Prediction of postoperative morbidity after lung resection using an artificial neural network ensemble. Artif Intell Med 2004;30:61-9. [Crossref] [PubMed]
- Feng F, Wu Y, Wu Y, et al. The effect of artificial neural network model combined with six tumor markers in auxiliary diagnosis of lung cancer. J Med Syst 2012;36:2973-80. [Crossref] [PubMed]
- Poullis M, McShane J, Shaw M, et al. Lung cancer staging: a physiological update. Interact Cardiovasc Thorac Surg 2012;14:743-9. [Crossref] [PubMed]
- Toney LK, Vesselle HJ. Neural networks for nodal staging of non-small cell lung cancer with FDG PET and CT: importance of combining uptake values and sizes of nodes and primary tumor. Radiology 2014;270:91-8. [Crossref] [PubMed]
- Naresh P, Shettar DR. Early Detection of Lung Cancer Using Neural Network Techniques. Int Journal of Engineering 2014;4:78-83.
- Chen J, Chen J, Ding HY, et al. Use of an Artificial Neural Network to Construct a Model of Predicting Deep Fungal Infection in Lung Cancer Patients. Asian Pac J Cancer Prev 2015;16:5095-9. [Crossref] [PubMed]
- Xie NN, Hu L, Li TH. Lung cancer risk prediction method based on feature selection and artificial neural network. Asian Pac J Cancer Prev 2014;15:10539-42. [Crossref] [PubMed]
- Pasini A, Modugno G. Climatic attribution at the regional scale: a case study on the role of circulation patterns and external forcings. Atmospheric Science Letters 2013;14:301-5. [Crossref]
- Bertolaccini L, Viti A, Boschetto L, Pasini A, et al. Analysis of spontaneous pneumothorax in the city of Cuneo: environmental correlations with meteorological and air pollutant variables. Surg Today 2015;45:625-9. [Crossref] [PubMed]
- Lisboa PJ. A review of evidence of health benefit from artificial neural networks in medical intervention. Neural Netw 2002;15:11-39. [Crossref] [PubMed]


