Multivariate analysis in thoracic research
Introduction
With the development of information technology and communication, it is now easier to make processes of collection, storage and transportation of large—both in volume and complexity—databases from observation or experimentation. A multivariate approach will help to illuminate the inter interrelatedness between and within sets of variables.
Definition
Multivariate analysis in a broad sense is the set of statistical methods aimed simultaneously analyze datasets. That is, for each individual or object being studied, analyzed several variables. The essence of multivariate thinking is to expose the inherent structure and meaning revealed within these sets if variables through application and interpretation of various statistical methods.
There are two determining factors that have to take into account when doing a multivariate approach (1): (I) the multidimensional nature of the data matrix and (II) the purpose of trying it, preserving its complex structure. This is based on the belief that the variables are interrelated, so that only the set of the same test may provide a better understanding of the studied object obtaining information univariate and bivariate statistical methods are unable to achieve. The joint treatment of the variables will faithfully reflect the reality of the problem addressed (2).
Types of multivariate methods
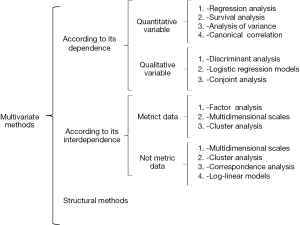
Multivariate methods can be classified based on the types of variables (3) (Figure 1):
- According to the methods of dependency: Analyzed variables are divided into two groups: dependent and independent variables. The aim is to determine whether the set of independent variables affects all dependent variables and how. They develop a hypothesis that attempts to validate empirically are explanatory or predictive techniques.
- If the dependent variable is quantitative, we can use different multivariate models such as:
- Regression analysis: It is typically used to predict the behavior of certain variables from others. Generally, it does not describe the relationship between variables because it ignores the possible random variations in the value of the independent variable and they are not derived from the variation of the dependent variables. An example would be to analyze a sample of 500 smokers aged 50 years and establish the relationship between lung cancer (outcome or dependent variable) and some of its basic characteristics and habits: number of cigarettes per day, number of years of smoking, forced expiratory volume at first second (FEV1), etc.
- Survival analysis: It consists of a set of appropriate statistical techniques where each subject is followed for a certain period. Here the independent variable is the time to the event (time to death for survival analysis, but also can be time to recurrence, time to discharge, etc.). This model will allow us to study the relationship between a set of explanatory variables and the incidence of the event of interest and also to predict the survival chances of a given subject from the pattern of values taken in the predictors. The most widely used model in health sciences is the proportional hazards model of Cox. An example would be a study for ex-smokers relapse (outcome variable) in their consumption according to their employment status, the presence of mental illness, if they have other toxic habits and years of smoking (explanatory variables).
- Analysis of variance: a method for comparing various measures in different situations that is used when the full sample is divided into several groups based on one or more non-metric independent variables and the dependent variables analyzed are metric. An example could be to evaluate the efficacy of different drugs to control dual bronchodilator chronic obstructive pulmonary disease (COPD), compared with inhaled corticosteroid and a bronchodilator drug in a population of patients with COPD; these patients were randomly distributed. The first group would be provided a placebo, the second an inhaled corticosteroid and a bronchodilator; the third, it would be administered twice bronchodilator therapy and the results are evaluated.
- Canonical correlation: it is based on to try to analyze simultaneously multiple dependent and independent metric variables by calculating linear combinations of each set of variables, looking for the possible existence of relationship between two sets of variables. Its objectives are to determine whether two sets of variables (measurements on the same objectives) are independent from each other or, conversely, to determine the magnitude of the relationships that may exist between the two sets. A possible example would be to determine if lifestyle and dietary habits have an effect on health by measuring different variables such as weight, blood pressure and dyslipidemia.
- If the dependent variable is qualitative:
- Discriminant analysis: it provides rules for classifying new observations of their group of origin, based on the information provided by the values it takes the independent variables. In other words, it indicates which variables differentiate the groups. The objective of this analysis is to find the linear combination of independent variables that best differentiate the groups. We would establish which patients would benefit and which lung cancers are not of a formal lobectomy—versus atypical resection—in stage I.
- Logistic regression models: Logistic regression measures the relationship between a categorical dependent variable and one or more independent variables, which are usually (but not necessarily) continuous, by using probability scores as the predicted values of the dependent variable (5). The aim would be to explore a set of possible predictors to define those that are important in explaining a particular dependent variable and build a prognostic index to predict response or outcome (Y) from a set of explanatory variables (X), help control the effects of confounding variables to estimate the specific effect of one or more factors (Xi) on a variable (Y), detect and assess interaction effects between two or more explanatory variables. The regression analysis may be applied for example in a study of lung cancer [dependent variable (Y)] from studying snuff consumption (X1), asbestos exposure (X2) and exposure to radon (X3).
- Conjoint analysis: It is a method that analyzes the effect of non-metric independent variables in metric or non-metric variables. Unlike the analysis of variance, the dependent variables may be non-metric and the analyst sets non-metric values of the variables. The goal is to understand how individuals form their preferences for objects or stimuli, estimating the relative importance attached to each of the attributes or characteristics of it. This model would explain the preferences of patients with lung cancer when choosing a treatment.
- According to the methods of interdependence: It is based in to do a reality approach without specific hypotheses and try to describe reality by synthesizing the relevant information; they are descriptive or reductive techniques. They can be classified into two groups based on whether the data analyzed are metric or non-metric.
- If the data are metric:
- Factor analysis and principal component analysis: this technique allows to analyze interrelationships among a large number of metric variables explaining these relationships in terms of a smaller number of variables called factors if they are unobservable or components if they are observable. It removes existing redundancies between the initial set of observed variables. A possible example would be to study a group of items from a scale and label them under a single dimension or factor assessment.
- Multidimensional scales: It transforms judgments of similarity or preference distances represented in multidimensional space. The objectives are: proximity between objects used to perform a spatial representation of them and identify the underlying dimensions. An example is the spatial representation of the similarities between the various chemotherapy treatments lung cancer in order to know the relative positioning of each of them.
- Cluster analysis: This is a method for ranking entities; whether individuals or variables in a small number of groups so that the observations within a group are very similar and very different from the rest. Unlike discriminant analysis, the number and composition of these groups is unknown. This method could build a sanitary map in Spain according to the incidence of the different types of lung cancer.
- If the data are not metric:
- Multidimensional scales.
- Cluster analysis.
- Correspondence analysis: It is applied to multidimensional contingency tables and pursues a similar multidimensional but simultaneously representing the rows and columns of the contingency tables scales goal. Its goals are to reduce the data (non-metric variables); from the relationship between observed variables, identifying dimensions or latent variables; deepen the relations established between two or more categorical variables. A possible example would be to get a perceptual positioning map showing the association between lung cancer and the underlying dimensions.
- Log-linear models: It is based on applying to multidimensional contingency tables and multidimensional relationships modeled dependence of the observed variables that seek to explain the noted frequencies. They allow the researchers to test different models that posit types of relationships between two or more categorical variables.
- Structural methods: These methods assume that the variables are divided into two groups: the dependent variables and the independent. They aim to analyze how the independent variables affect the dependent variables and the relationships of the variables in the two groups together. For example, consider how the resources of the fast lane of lung neoplasms with perceptions that patients have of it are used.
They can be classified according to if the dependent variable or variables are quantitative or qualitative (4).
Stages of realization of a multivariate analysis
The steps (I) to perform a multivariate analyze can be summarized in:
- State the objectives of the analysis. Define problem in its conceptual terms, objectives and multivariate techniques that are going to be employed.
- Design analysis. To determine the sample size and estimation techniques those are going to be employed.
- Decide what to do with the missing data.
- Perform the analysis. Identify outliers and influential observations whose influence on the estimates and goodness of fit should be analyzed.
- Interpret the results. These interpretations can lead to redefine the variables or the model which can return back to steps (III) and (IV).
- Validate the results. At this point, we must establish the validity of the results obtained by analyzing other results obtained with the sample is generalized to the population from which it comes.
Multivariate analysis example
Wells et al. (6) published in New England Journal of Medicine a study were they hypothesized that a computed tomographic (CT) metric of pulmonary vascular disease [pulmonary artery enlargement, as determined by a ratio of the diameter of the pulmonary artery to the diameter of the aorta (PA: A ratio) of >1] would be associated with previous severe COPD exacerbations . A univariate logistic regression was used to determine the associations between patient characteristics (including the PA: A ratio) and the occurrence of a severe exacerbation of COPD in the year before enrollment. Variables showing a univariate association with severe exacerbations (at P<0.10) were included in stepwise backward multivariate logistic models to adjust for confounders. These models included also variables previously reported to be independently associated with acute exacerbations of COPD in the ECLIPSE study as gastro-esophageal reflux disease (GERD), lower values for the forced expiratory volume in 1 second (FEV1), a history of acute exacerbations of COPD within the previous year, increased white-cell count, and decreased quality of life as measured by the St. George’s Respiratory Questionnaire (SGRQ) score (which ranges from 0 to 100, with higher scores indicating worse quality of life and with a minimal clinically important difference of 4 points). Authors found significant univariate associations between severe exacerbations and younger age, black race, use of supplemental oxygen, congestive heart failure, sleep apnea, thromboembolic disease, GERD, asthma, chronic bronchitis, employment in a hazardous job. Thanks to the development of a multivariate model, it will not only let to handle many covariates, it will let to asses potential confounders and also test for interaction or effect modification. Multiple logistic-regression analyses showed continued significant independent associations between severe exacerbations and younger age, lower FEV1 values, higher score on the SGRQ, and a PA: A ratio of more than 1.
Conclusions
This article provides a brief overview of the importance of using multivariate studies in the health sciences and the different types of existing methods and their application depending on the type of variables to deal with. In addition, it described the steps to follow to design a multivariate study.
Acknowledgements
Disclosure: The authors declare no conflict of interest.
References
- Gil Pascual JA. Methods worth of research in education. Multivariate Analysis 2003.
- Grimm LG, Yarnold PR. eds. Reading and understanding multivariate statistics. Washington, DC: American Psychological Association Washington, 2011.
- Rencher AC, Christensen WF. eds. Methods of Multivariate Analysis. New Jersey: Wiley, 2012.
- Afifi A, May S, Clark VA. Practical Multivariate Analysis, Fifth Edition. Boca Raton, FL: CRC Press, 2011.
- Chan YH. Biostatistics 202: logistic regression analysis. Singapore Med J 2004;45:149-53. [PubMed]
- Wells JM, Washko GR, Han MK, et al. Pulmonary arterial enlargement and acute exacerbations of COPD. N Engl J Med 2012;367:913-21. [PubMed]