P value interpretations and considerations
Introduction
The use of statistics in surgical literature has increased over the last few decades (1). The P value has been in use for nearly a century (2). P values are found in virtually all scientific literature and are used by researchers and clinicians to show the statistical significance of relationships between two groups for a specific variable (3).
The P value is the probability of rejecting or failing to reject the null hypothesis (H0) (4). H0 is the hypothesis that there is no difference between two groups for a specific variable. The “P” in P value stands for probability. A P value is calculated as the probability that an observed effect as large or larger if H0 is true. The P value measures the strength of evidence against H0 (5). The smaller the P value, the stronger the evidence against H0. For example, a recent trial evaluating extended postoperative antibiotic prophylaxis for elective thoracic surgery calculated a P value of 0.26 comparing patients receiving an extended antibacterial prophylaxis and those receiving standard preoperative prophylaxis only (6). This P value can be interpreted as a 26% chance that there would be results this extreme or more extreme if there was no difference between receiving the extended antibiotic prophylaxis as compared to the standard prophylaxis regimen in this study. The authors conclude that “extended postoperative antibacterial prophylaxis for patients undergoing elective thoracic surgery requiring tube thoracostomy did not reduce the number of infectious complications compared with preoperative prophylaxis only” (6). If the study calculated a P value of 0.01 for the difference in infectious complications between the two groups, a 1% chance that there was a observed difference that happened randomly between the treatments if there is not a true difference in infectious complications, researchers would reject the H0 and state that there is a statistically significantly difference in infectious complications between the two groups. A P value should be compared to an a priori determined alpha (α) level in order to conclude statistical significance to reject the H0 and state that there is a difference between groups. It should be noted that a P value should not be simply dichotomized as to above or below the α level, but should be interpreted as part of the entire research study process which includes sample size, participant selection, and measures of both treatment and outcome (7).
Setting an α level
α level is the amount of type I error you are willing to accept. It should be determined a priori, that is before enrolling study participants of collecting data. The most commonly used α level is 0.05, as proposed by Fischer, however there may be some situations where the α level is smaller or larger (2). A type I error is where the H0 is falsely rejected, or that researchers state that there is a difference when in truth there is not. There may be some situations where researchers need to be more certain that there is a difference between groups, such as if a new untested and potentially harmful treatment is meaningfully better than a simple, noninvasive treatment with demonstrated efficacy and safety, as was the case in a recent study evaluating vaccine safety (8). This study utilized an α level of 0.01 for some of their analyses. Other situations where a modified α level may be justified include (I) assessment of effect modification by a third variable on the relationship between the treatment and outcome or (II) adjustments for multiple comparisons within the same study. In nearly all biomedical research, the α level for primary analyses is nearly always 0.05.
When assessing for effect modification, which is the impact of a third factor on the treatment-outcome relationship, it is increasingly acceptable to relax the α level to a higher value, typically 0.10 or 0.15, but in some instances as high as 0.20. As an example, the third variable could be the impact of age on the relationship between extended antibiotic prophylaxis as compared to standard pre-surgical antibiotic prophylaxis. If the researchers believe that older patients are more likely to respond to an extended treatment regimen as compared to younger patients, then they would assess for effect modification of age on the relationship between prophylaxis and infectious complications. This relaxation of the acceptable level of type I error for the effect modification should be based on how willing the researchers are to conclude that a third variable, in this example age, has a meaningful effect on the relationship between extended prophylaxis and infectious complications.
Multiple comparisons are commonly performed in a single biomedical research study. There is debate about the application and level of statistical adjustment of statistical significance when multiple comparisons are made within a single study (9,10). Multiple types of adjustment for multiple comparisons exist, and include Bonferroni, Sidak, Dunnett, Holm and others. While each adjustment is for a specific type of test or situation, all operate in generally the same way, to lower the likelihood of committing a type I error. It is considered best practice to adjust for multiple comparisons and therefore be more conservative in conclusions, however there is no uniform agreement on when to adjust or what type of adjustment best.
Regardless of the application, a P value is a tool to help interpret findings from biomedical research and determine if practice can be improved.
Statistical versus clinical significance
Fisher suggested 5% (α=0.05) level could be used for concluding that fairly strong evidence exists against H0, that is 1 out of 20 times you will be wrong and by random chance there is no difference between your groups, but the data you have suggests that there is (2). It has become scientific convention to say that P>0.05 aren’t strong enough to reject the H0 (11), however the P value was no intended as an absolute threshold. Strength of evidence is on a continuum and simply noting the magnitude of the P value doesn’t suffice. A P value may show that a relationship between two effects is statistically significant where the magnitude of the difference between the effects is small. While this difference may be statistically significant, it may not be clinically significant.
Keep in mind that the α level is an arbitrary cut-point. Scientific and clinical context is critical in differentiating statistical significance from clinical significance. A P value alone conveys little information about a study’s results (12) and even precise P values don’t show anything about the magnitude of effect, the differences in variables between study groups (12). The use of confidence intervals provides researchers with a range of values rather than an arbitrary “significant vs. non-significant” value (12). Studies have advocated for the use of confidence intervals to show a range of values that are considered for a sample (13,14). However, the use of a P value is helpful in addition to a confidence interval and ideally both should be presented.
Reporting of the actual P value, not a categorized P>0.05 or P≤0.05 is important. A P value of 0.051 is nearly the same to a P value of 0.049, however the first has traditionally been disregarded when in fact it may be clinically significant, but have study design elements which negatively affected the P value. Consideration of low P values (e.g., P<0.10) as “trending toward statistical significance” may be clinically relevant for improving practice, particularly in smaller studies.
Study design elements which can impact a P value
Multiple study design elements can have an impact on the calculated P value. These include sample size, magnitude of the relationship and error. Each of these elements may work independently or in concert to invalidate study results.
Error and its effect on P value
There are two types of error that can impact a P value: (I) random error and (II) systematic error (3,7,15). Random error is defined as variability in data that is not readily explained, essentially random noise both above and below the “true” value. A random error is not considered a bias but rather occurs random across the entire study population and can distort the measurement process. An example of random error may occur when measuring the height of a study population. The each individual height measure may randomly differ (up or down) from the true height depending on the way it was held, how it was read, or the researcher who took the measurement. If the way the measuring tape was held differently was random, then the resulting errors will be random. The more study participants are included in these measurements, the smaller the effect of error will become. Random error biases the true relationship towards the H0 of what is being studied, or makes it less likely to find statistically significant associations. If, for example, a researcher finds no statistical differences between two groups and random error is present, that random error may have caused the true relationship to be biased toward the null. Random errors are best avoided in the study planning phase and by including a large sample size. The larger the sample size of the study population the less likely it is to have random error present (see Figure 1).
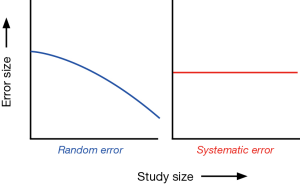
Systematic error is a bias and can alter the observed association in either direction, therefore making a result “statistically significant” when it truth it is not, or deleteriously impacting a true relationship to appear to be statistically insignificant. Three major types of biases need to be considered: (I) selection bias; (II) information bias; and (III) confounding.
Selection bias may be present when individuals have different probabilities of being included in the study sample. For example, subjects may be more likely volunteer to participate in new investigational drug to treat their disease if they have failed past treatments or have advanced disease and would be more likely to report successful treatment. These issues may equate to study population that has a built in predisposition for a specific outcome and may make a study statistically significant, when in truth there is no difference in treatments. This can also work in the other direction, where participants are more likely to report a treatment as being not successful based on their past experience.
Information bias involves a systematic tendency for subjects selected for inclusion in the study to be erroneously placed in different exposure/outcome categories which can lead to misclassification. The most common type of information bias is recall bias. Asking study subjects to recall information from the past may lead to biased information if there is a stigma or reason why someone would over or under report the truth (e.g., reporting more exercise than what actually occurs or underreporting smoking history or drug use because of societal pressures). Information bias might be introduced by the interviewer phrasing study questions differently with each study subject.
Lastly, confounding can mask, inflate or deflate the true estimate of the exposure outcome relationship (3). Confounding is present when a third variable is related to both, the exposure and the outcome.
Systematic errors can either falsely raise or falsely lower the estimate of risk. For example, if researchers measure the weight of a study population and the scale measures everyone 2 pounds heavier. The data distribution of the weight measurements would shift in one direction and be overestimated systematically. Increasing the sample size will have no effect on this systematic bias (Figure 1).
Sample size and magnitude of effect
A P value is also affected by sample size and the magnitude of effect. Generally the larger the sample size, the more likely a study will find a significant relationship if one exists. As the sample size increases the impact of random error is reduced. Additionally, the overall variability is decreased, and measures become more precise for a population as a whole. This increased precision allows for detection of smaller and smaller differences between groups. The magnitude of differences between groups also plays a role. If there is a large magnitude of difference then it will be easier to detect (16). If there are two studies with equal sample sizes which are free of error measuring two different relationships, the relationship with the larger magnitude of effect (e.g., difference between groups) will have a small P value as compared to the study with the smaller magnitude of effect.
Conclusions
P values are a useful tool for interpreting research findings and continuing to improve medical practice. However, P values should be considered as a spectrum, not a binary significant or non-significant metric. Similarly, issues such as sample size, magnitude of effect, and potential for random error, systematic error and confounding should all be considered in tandem with the P value itself.
Acknowledgements
Funding: This study has been funded, in part, by grants from the National Institute for Occupational Safety and Health (NIOSH/CDC) Education and Research Center training grant T42/CCT810426-10. The CDC/NIOSH is not involved in this manuscript.
Footnote
Conflicts of Interest: The authors have no conflicts of interest to declare.
References
- Derossis AM, DaRosa DA, Dutta S, et al. A ten-year analysis of surgical education research. Am J Surg 2000;180:58-61. [Crossref] [PubMed]
- Fisher RA. Statistical methods for research workers. 11th ed. Biological monographs and manuals. No. V. Edinburgh: Oliver and Boyd, 1950:1-354.
- Lang JM, Rothman KJ, Cann CI. That confounded P-value. Epidemiology 1998;9:7-8. [Crossref] [PubMed]
- Boos DD, Stefanski LA. P-Value Precision and Reproducibility. Am Stat 2011;65:213-21. [Crossref] [PubMed]
- O'Brien SF, Osmond L, Yi QL. How do I interpret a p value? Transfusion 2015;55:2778-82. [Crossref] [PubMed]
- Oxman DA, Issa NC, Marty FM, et al. Postoperative antibacterial prophylaxis for the prevention of infectious complications associated with tube thoracostomy in patients undergoing elective general thoracic surgery: a double-blind, placebo-controlled, randomized trial. JAMA Surg 2013;148:440-6. [Crossref] [PubMed]
- Greenland S, Senn SJ, Rothman KJ, et al. Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations. Eur J Epidemiol 2016;31:337-50. [Crossref] [PubMed]
- Lee GM, Greene SK, Weintraub ES, et al. H1N1 and seasonal influenza vaccine safety in the vaccine safety datalink project. Am J Prev Med 2011;41:121-8. [Crossref] [PubMed]
- Goodman SN. Multiple comparisons, explained. Am J Epidemiol 1998;147:807-12. [Crossref] [PubMed]
- Drachman D. Adjusting for multiple comparisons. J Clin Res Best Pract 2012;8:1-3.
- Thisted RA. What is a P-value? 1998:1-6. Available online: http://www.stat.uchicago.edu/~thisted/
- Gardner MJ, Altman DG. Confidence intervals rather than P values: estimation rather than hypothesis testing. Br Med J (Clin Res Ed) 1986;292:746-50. [Crossref] [PubMed]
- Analyzing data from ordered categories. N Engl J Med 1984;311:1382-3. [Crossref] [PubMed]
- Rothman KJ. A show of confidence. N Engl J Med 1978;299:1362-3. [Crossref] [PubMed]
- Rothman KJ, Lash TL, Greenland S. Modern Epidemiology. Philadelphia: Lippincott Williams & Wilkins, 2008.
- Rothman KJ. Epidemiology: an introduction. Oxford: Oxford University Press, 2012.


